Undersøgende og eksperimenterende matematik
Der er mange forskellige elementer i matematikundervisningen. Den undersøgende og eksperimenterende matematik er på mange måder toppen af kransekagen. I den undersøgende og eksperimenterende matematik kommer mange kompetencer i spil, endda på en måde som gør eleverne til bedre samfundsborgere.
Hvad er undersøgende matematik?
Al matematikundervisning rummer en lang række forskellige aktiviteter, som eleverne arbejder med selvstændigt eller i grupper. Aktiviteterne kan for eksempel vurderes ud fra tre dimensioner: Graden af åbenhed, inddragelse af virkelighed og kompleksitet i problemløsning.
Undersøgende matematik er aktiviteter, hvor det centrale er, at eleverne selv stiller matematiske spørgsmål og træffer valg, der har matematisk betydning for arbejdet med aktiviteten.Undersøgelser kan inddrage virkelighed, men behøver det ikke. Der er masser af spændende undersøgelser, som alene lever i matematikkens verden.
En god undersøgelse kan ofte starte lukket, og det er elevernes nysgerrighed og spørgsmål der – godt støttet af læreren – åbner undersøgelsen. Se for eksempel FP9 maj 2018, opgave 6.3 og 6.4.

Opgave 6.3 starter med ordet “Undersøg”. Der er ikke meget undersøgelse over opgaven i sig selv, den kunne lige så godt være formuleret ”Kan denne graf være en ret linje? Du skal begrunde dit svar.” Men når den følges op af opgave 6.4 lægges der op til en god undersøgelse. Eleverne kan stille sig selv spørgsmål om forskriften for funktionen med grafen gennem de tre punkter, de kan vælge om de vil finde andre forskrifter for andre lineære funktioner gennem (0,0), og de kan overveje forskrifter for ikke-lineære funktioner gennem (0,0), og om der er nogle fællestræk ved funktioner gennem (0,0).
Hvad er eksperimenterende matematik?
At eksperimentere er at prøve noget nyt for at samle erfaringer. Det vil vi naturligvis meget gerne fremme i matematikundervisningen, men man skal være bevidst om, hvad man bruger eksperimenter til i matematik. Det er noget andet end i f.eks. fysik/kemi eller biologi.
Matematikerens rolle ift eksperimenter er at systematisere de opnåede erfaringer: Lede efter mønstre og opstille hypoteser om matematiske sammenhænge.
Når erfaringerne handler om omverdenen, opstilles hypoteserne som modeller, der kan afprøves eksperimentelt. Men er erfaringerne om ren matematik, er hypoteserne netop blot hypoteser om matematiske regler, der ikke kan eftervises eksperimentelt, men hvor man skal ræsonnere sig frem til rigtigheden og argumentere gennem matematikken selv.
Man kan eksperimentere med, hvor meget vand der kan være i sugerør af forskellig længde. Ved at se på de data man samler op, kan man lave en model for, hvilken sammenhæng der er mellem sugerørets længde og mængden af vand.
Denne model kan man afprøve med nogle andre sugerør. Den matematiske hypotese er en model, der kan efterprøves eksperimentelt.
Man kan eksperimentere med at tegne en masse femkanter og finde vinkelsummen af dem. Tegner og måler man i hånden, kommer disse vinkelsummer nok til at ligge et sted mellem 530 og 550 grader, og laver man det i GeoGebra, kommer de nok til at ligge på 540 grader hver gang. En naturlig hypotese er, at vinkelsummen i en femkant er 540 grader.
I matematikken er det ikke bevist, bare fordi det gælder for alle de eksempler man har prøvet. Matematik er ikke et eksperimentelt fag. Eksperimenterne kan bruges til at se mønstre og få gode ideer til at formulere hypoteser, men rigtigheden skal man ræsonnere sig frem til.
For vinkelsummen i en femkant kan man bruge det argument, at enhver femkant kan deles op i tre trekanter ud fra et hjørne. Vinkelsummen af de tre trekanter er da lig med vinkelsummen af femkanten. Vi ved, at vinkelsummen af en trekant er 180 grader, så vinkelsummen af en femkant er 3*180=540 grader.
Man kan undersøge antallet af divisorer i tallene frembragt af de to polynomier n2+n+41 og n2+n. For eksempel er de første tre tal frembragt af n2+n+41 (for n=1, 2 og 3) 43, 47 og 53, der alle kun har to divisorer nemlig 1 og tallet selv. De første tre tal frembragt af n2+n (2, 6 og 12), har to divisorer (1 og 2 går op i 2), fire divisorer (1, 2, 3 og 6 går op i 6) og seks divisorer (1, 2, 3, 4, 6 og 12 går op i 12). Man kan eksperimentere videre og sætte flere tal ind i de to polynomier og det kan give anledning til at stille nogle matematiske spørgsmål, måske ligefrem opstille nogle hypoteser: Frembringer n2+n+41 altid tal med netop to divisorer, altså primtal? Og hvis den stopper med at frembringe primtal, hvornår sker det så? Frembringer den alle primtal op til et vist primtal eller springer den over nogle? Frembringer n2+n aldrig primtal? Og i givet fald hvorfor? Frembringer den tal med flere og flere divisorer?
Regneark er et godt hjælpemiddel til denne undersøgelse. Både til at frembringe de relevante tal med polynomierne og til at finde antallet af divisorer ved at undersøge om division med kendte primtal giver hele tal.
Undersøgelsen er en god anledning til at snakke om, hvordan man finder ud af rigtigheden af matematiske hypoteser. Det er ikke nok at prøve én gang, eller to gange eller ti gange for at vise rigtigheden af noget, til gengæld er ét modeksempel nok til at afvise en hypotese. Og et matematisk ræsonnement kan bevise hvad aldrig så mange eksempler ikke kan.
n2+n+41 frembringer primtal for n=0 til 39 for n=40 giver det 1681, som er 412. n2+n+41 giver oplagt heller ikke et primtal for n=41, da 41 går op i alle tre led. n2+n+41 giver ikke alle primtallene op til 1681, for eksempel rammer den ikke 59.
n2+n frembringer ikke andre primtal end 2 (for n=1). n2+n kan skrives om til n*(n+1), hvormed man kan se, at både n og n+1 altid er divisorer. Heraf kan man også se, at 2 altid er divisor, da 2 enten går op i n eller n+1. n2+n frembringer ikke tal med flere og flere divisorer for eksempel giver n=16 tallet 272 som har ti divisorer og n=22 giver tallet 506, som kun har otte divisorer.
Hvorfor er undersøgende og eksperimenterende matematik vigtigt?
Undersøgende og eksperimenterende aktiviteter arbejder med de fire kompetencer der handler om at spørge og svare i, med og om matematik:
- Tankegangekompetencen: Hvilke spørgsmål kan man stille i og med matematik?
- Ræsonnementskompetencen. Hvis man gør sådan og sådan, hvad sker der så – og hvorfor?
- Modelleringskompetencen. Hvordan kan man beskrive omverdenen med matematik – og hvor godt passer det?
- Problembehandlingskompetencen, specielt den del der handler om at opstille matematiske problemer.
Skolen skal lære eleverne at være aktive og nysgerrige. Det er eleverne som skal lære noget og derfor dem, der skal være aktive. Undersøgende og eksperimenterende matematik aktiverer elever, og eleverne tager øget ejerskab, fordi de selv er med til at forme hvilken retning aktiviteten går i.
Man kan træne matematisk nysgerrighed ved at lege “Hvor mange og hvad”. Læg nogle genstande, fx 5 møtrikker, i en dåse. Eleverne skal gætte antallet af genstande og hvilke genstande der er, ved at stille spørgsmål, som kan besvares med ja eller nej.
Læreren starter med at gennemgå de fem slags spørgsmål, man kan stille:
De tre matematiske spørgsmål, “hvor mange”, “hvor stor” og “hvilken form”.
Ingeniør-spørgsmålene om funktion, materialer og egenskaber.
Humanist-spørgsmålene om følelser og relationer.
Klassen diskuterer hvilke spørgsmål man kan stille, når nu ikke man bare kan spørge direkte. “Er der mere end 10?”, “er de længere end 5 cm på den længste led?”, “er de kantede?”, “er de lavet af metal?”, “bruges de til at lave mad med?” osv.
Der er masser af mulige spørgsmål til både de dygtige og de mindre dygtige, til de engagerede og til de, der er lidt ligeglade.
Det er vigtigt at bruge aktiviteten flere gange. Gør man det en gang, er det underholdning, gør man det flere gange, bliver det undervisning. Når aktiviteten bruges flere gange, bliver eleverne bedre til at stille spørgsmål og bedre til at bruge andres spørgsmål og svar. Og eleverne opdager selv, at de bliver bedre.
Når man senere i livet skal bruge matematik derhjemme eller på arbejde finder man den aldrig i form af opstillede regnestykker. I virkeligheden skal man altid stille sig selv spørgsmål og træffe valg før man finder ud af, hvad det egentlig er man vil regne på. Det er meget nemmere at finde ud af, hvis man allerede i skoletiden har eksperimenteret med matematikken.
Det er ikke tilstrækkeligt at kunne matematik. Det er først nyttigt, når man også har viljen og modet til at bruge matematik. Rigtig mange mennesker tør ikke bruge matematik. Vi tror at det bl.a. skyldes, at de er opvokset under et matematisk opgaveparadigme, hvor læreren eller lærebogen stiller opgaver, hvor der kun er ét rigtigt svar og en milliard forkerte. I det paradigme er det ikke op til eleven selv at afgøre om svaret er korrekt, det er læreren eller den matematikgud, der skrev bogens facitliste der afgør det. Fejl er en dårlig præstation, og et tegn på, at man ikke kan finde ud af det. Fejl er ikke et skridt på vejen. Undersøgende og eksperimenterende matematik vender dette på hovedet, og hjælper med at etablere en nødvendig ny didaktisk kontrakt.
En ny didaktisk kontrakt
Den didaktiske kontrakt er de uskrevne regler om, hvordan man opfører sig i matematikundervisningen. Den gamle kontrakt, som desværre lever i bedste velgående hos mange elever og forældre er:
- Det er godt at være hurtig færdig.
- Det er godt, når man ikke behøver stille spørgsmål.
- Der er ét rigtigt svar.
- Man skal ikke selv bestemme noget i opgaverne.
- Det er forbudt at kikke ved andre.
- Læreren kan altid forklare hvad man skal.
Den kontrakt trænger i den grad til at blive udskiftet til en, der matcher nutidens krav. Vores forslag er følgende:
- Det er godt at fordybe sig og blive længe i samme opgave.
- Det er godt at stille flere spørgsmål.
- Man skal selv bestemme noget i opgaverne.
- Det er godt at komme med mange forskellige svar.
- Det er godt at bygge videre på andres svar.
- Læreren har ikke alle svar.
- Læreren stiller spørgsmål, så man selv kan tænke videre.
Barrierer
Hvis det er så godt at arbejde undersøgende og eksperimenterende, hvorfor er det så ikke mere udbredt?
Det er meget nemmere at tage næste side i lærebogen end det er at arbejde undersøgende og eksperimenterende. Det tager tid for læreren at sætte sig ind i undersøgelser eller eksperimenter, og i mange situationer kræver det også, at der skal findes nogle materialer frem.
Skiftet til den ny didaktiske kontrakt kan skabe usikkerhed og kaos hos eleverne. Det er også en usikker situation for læreren, der lige pludselig ikke har svar på alle de spørgsmål, der dukker op. Hvis man er vant til at være eksperten, der ved alting, er det en omstilling at skulle til at ræsonnere sammen med eleverne eller måske undersøge spørgsmålene selv.
Endelig kræver dette arbejde mod og tro på et andet matematiksyn end det traditionelle. Traditionens vogtere er utallige, og synes flere og flere i disse år. Mængden af test og krav til karakterer har det med at presse tilbage mod de gamle dyder og gøre lysten til fornyelse mindre.
Hvordan kommer det til at lykkedes?
I mange lærebøger sker der desværre nogle kæmpe spring fra lukkede opgaver til vildt åbne modelleringer. For at lykkes med undersøgende og eksperimenterende matematikundervisning skal man som lærer være tryg ved situationen. Den tryghed kan opnås ved at starte med små enkle åbne opgaver, og stille og roligt vænne eleverne og sig selv til den nye didaktiske kontrakt.
Den ny didaktiske kontrakt skal italesættes. Elever vil gerne gøre det rigtige, så når forventningerne til, hvad der er rigtigt ændres, skal det kommunikeres meget tydeligt. Man vil måske også opleve, at det er andre elever, som nu bliver de mest aktive i timerne.
Vi har skrevet en artikel, som introducerer arbejdet med undersøgende matematik. Hvis man har lyst til mere inspiration, er vores bog ”Åben og undersøgende matematik” proppet med gode råd om, hvordan man kommer i gang og en masse eksempler på åbne opgaver.
Når klassen er vant til åbne og undersøgende opgaver, kan man gå videre til modelleringsarbejdet og den eksperimenterende matematikundervisning. Her er det om muligt et endnu større arbejde selv at finde på gode modeller, og i al beskedenhed kan vi igen anbefale vores egen bog ”Modellering og estimering i matematikundervisningen”.
Når man har afprøvet nogle åbne opgaver eller undersøgelser, som virker godt, skal man endelig gemme dem, så man kan bruge dem igen næste år. Og del meget gerne ud til kolleger. Nogle undersøgelser er bare bedre end andre, og det er vigtigt at få spredt de gode ud til så mange elever som muligt.
De skriftlige afgangsprøver har de sidste flere år støttet udviklingen hen imod mere åben og undersøgende matematik. Man kan godt diskutere om ikke det åbne og undersøgende hører bedre hjemme i den mundtlige prøve, der både muliggør løsere formuleringer og giver mere tid til undersøgelser. Men så længe myndigheder signalerer, at de skriftlige prøver er vigtigere end den mundtlige, så er det vigtigt at opgavekommissionen viser retningen, og lader de skriftlige prøver pege i en åben og undersøgende retning.

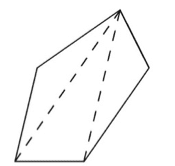 For vinkelsummen i en femkant kan man bruge det argument, at enhver femkant kan deles op i tre trekanter ud fra et hjørne. Vinkelsummen af de tre trekanter er da lig med vinkelsummen af femkanten. Vi ved, at vinkelsummen af en trekant er 180 grader, så vinkelsummen af en femkant er 3*180=540 grader.
For vinkelsummen i en femkant kan man bruge det argument, at enhver femkant kan deles op i tre trekanter ud fra et hjørne. Vinkelsummen af de tre trekanter er da lig med vinkelsummen af femkanten. Vi ved, at vinkelsummen af en trekant er 180 grader, så vinkelsummen af en femkant er 3*180=540 grader.



