Facebook og Instagram er fyldt med dem, de sniger sig ind i lærebøgerne og sågar i de afsluttende prøver: Ligningssystemer med billeder af alt fra hestesko til cola.

Der er mange, der holder af at pusle med ligningssystemer, og det er da dejligt at folk synes det er sjovt at løse ligninger i deres fritid.

Fra pusleri til matematik

Når vi som matematiklærere hiver disse ligningssystemer med billeder ind i undervisningen, skal vi gøre det til matematik og ikke bare puslerier. Matematik er krykstokke for hjernen, matematik skal hjælpe der, hvor vores egen hjerne ikke slår til. Vi skal gribe ned i matematikkens store værktøjskasse og finde værktøjer, som kan hjælpe. Og som kan hjælpe hver gang vi støder på tilsvarende problemer. Heldigvis er der flere gode muligheder.

Pusl, tænk og skriv ned

Det er oplagt at starte med at lade eleverne pusle, og så bede dem reflektere over hvad de gjorde og fortælle om deres strategier. Som lærer er det helt centralt, at man samler de matematiske pointer op i fællesskab, og fx laver plakater med strategier og eksempler på brug af dem. Og så skal eleverne have lov at anvende deres nye læring på andre ligningssystemer – og igen samle op og tilføje nye strategier eller nuancere allerede beskrevne strategier.

Brug matematikkens sprog

Matematik er også et sprog. Et sprog som netop er beregnet til at gøre uoverskuelige problemer overskuelige. Med matematikkens sprog udtrykker man de ubekendte med bogstaver og udtrykker sammenhængen mellem de ubekendte med symbolerne for de fire regningsarter. Bogstaverne for de ubekendte kan i første omgang være hele ord som ”cola” eller ”hest”, senere kan man gå over til det mere traditionelle matematiske brug af enkelt bogstaver som c og h, x, y, z, a, b, c eller hvad der nu passer bedst. Nogle af sådanne ligningssystemer med billeder bruger en mellemting mellem rene billeder og kombinationer af billeder og regningsarter. For eksempel i ligningssystemet med hestesko, hvor to hestesko ved siden af hinanden betyder plus mellem dem. Det er en fin mellemstation til de rent abstrakte ligningssystemer.

Brug CAS-systemer

En vigtig pointe med at omformulere ligningssystemer med billeder til symbolske ligningssystemer er, at man så kan anvende et CAS-værktøj til at løse ligningssystemet. Et nyttigt værktøj at kende til, når ligningssystemerne bliver store og tallene ikke længere er små og pæne.

Hvordan løser man ligninger?

Den overordnede strategi er, at man prøver at finde eller skabe ligninger, hvor der kun er én ubekendt. Så kan man nemlig løse den ligning og finde værdien af denne ubekendte.

Herefter kan man sætte den værdi ind i de andre ligninger, så der opstår flere ligninger med kun én ubekendt og på den måde finde værdier for alle de ubekendte.

Der er groft sagt to måder at lave få skabt ligninger med kun én ubekendt:

1. Man kan prøve at udtrykke en ubekendt ved hjælp af de andre ubekendte, og så indsætte dette udtryk i de andre ligninger.
2. Man kan gange en ligning med et tal ved at gange med samme tal på begge sider af lighedstegnet. Derefter kan man finde forskellen mellem denne ligning og en af de andre ligninger, og derved få ryddet ud i antallet af ubekendte.

Endelig er ”gæt og prøv efter” altid en mulig strategi. Man kan lave et kvalificeret gæt – fx ud fra et gennemsnit at de indgående variable, sætte ind i ligningerne og justere på værdierne. Gæt og prøv efter kræver at man er systematisk og god til at holde orden, så man ikke prøver de samme gæt flere gange, og så man opdager, om justeringerne bringer en nærmere løsningen. 

Det er for øvrigt tankevækkende, at noget så virkelighedsfjernt som ”to hestesko minus et par støvler lig med 2” er motiverende for mange mennesker. Det understreger, at vi ikke skal tro at matematik nødvendigvis skal være anvendelsesorienteret for at være motiverende.

Et par eksempler på løsninger

Eksempel 1

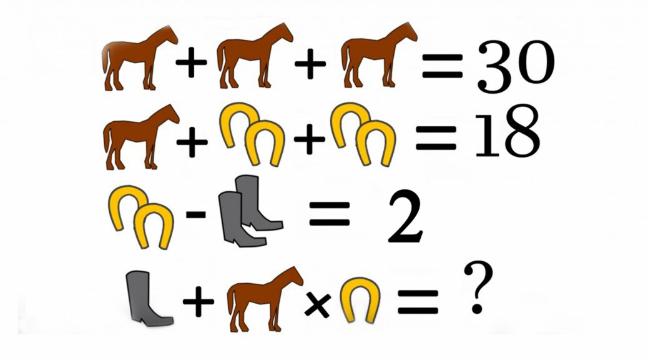
Find en ubekendt ad gangen

Når 3 heste er 30, må én hest være 10. Det bruger vi i næste ligning.

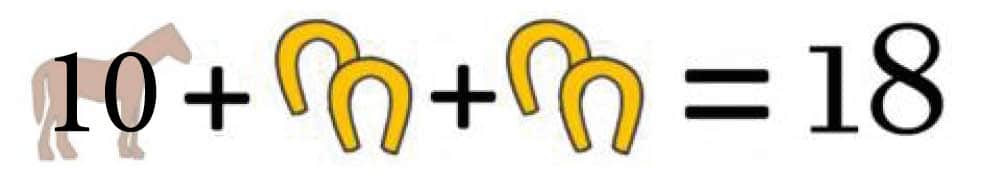
De to par hestesko må da være 8, for at lighedstegnet holder. Et par hestesko må da være det halve, altså 4. Det bruger vi i næste ligning.

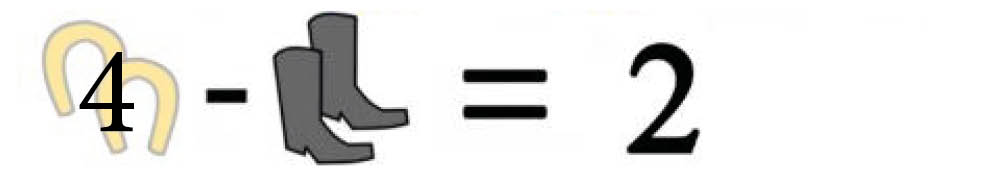
Så må et par støvler være 2, for at lighedstegnet holder. Og én støvle er da det halve, nemlig 1. Ligeledes er én hestesko det halve af 4, nemlig 2. Det bruger vi nu til at regne det sidste ud:

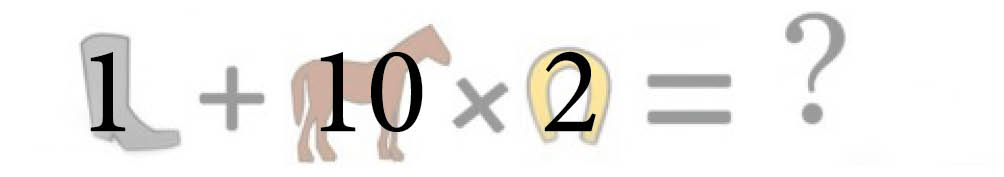
Svaret er 21.

Symbolsk – løst med CAS

Jeg bruger h for hest, s for hestesko og b for støvler (boots)

Eksempel 2

Gange én ligning op

Man kan gange den ene portion op, så man kan trække den anden portion fra igen og ende med kun slik eller cola. Det kan man gøre gennem tegningerne:

Eller stillet op anderledes:

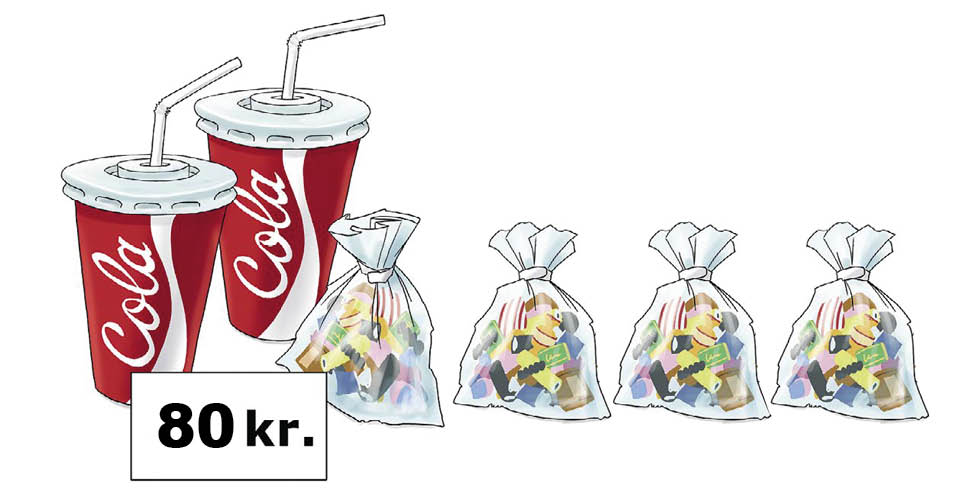
Bruger vi så den anden portion

ser vi, at de tre poser slik må koste 80 – 44 = 36 kr, og det betyder, at en pose slik koster 36 : 3 = 12 kr.

Den oplysning kan vi så gå tilbage og bruge i en af portionerne, fx denne:

Colaen må koste 40 kr. minus 2 poser slik til 12 kr. pr pose. Colaen koster altså 40 – 2 * 12 = 16 kr.

Gæt og prøv efter

Der er ikke stor forskel på om man køber 2 poser slik og 1 cola eller 1 pose slik og 2 colaer. Det ser ud til at 3 ting cirka koster 40-44 kr. lad os sige 42, det går 3 op i dvs. ca 42 : 3 = 14 kr. stykket.

Det passer jo selvfølgelig ikke at de koster det samme, så lad os lige korrigere inden vi prøver efter. Vi kunne jo sige 13 kr. for slik og 15 kr. for cola. Det giver for 2 poser slik og 1 cola: 2 * 13 + 15 = 41, det dur ikke. Det kunne jeg jo også have sagt mig selv, da tre ulige tal lagt sammen giver et ulige, og det skal give et lige, så jeg prøver med lige tal. 12 kr. for slik og 16 kr. for cola. Det giver for 2 poser slik og 1 cola: 2 * 12 + 16 = 40, det dur! Og 1 pose slik og 2 colaer giver 12 + 2 * 16 = 44, det dur også, så det er den rigtige løsning.

Symbolsk – løst med CAS

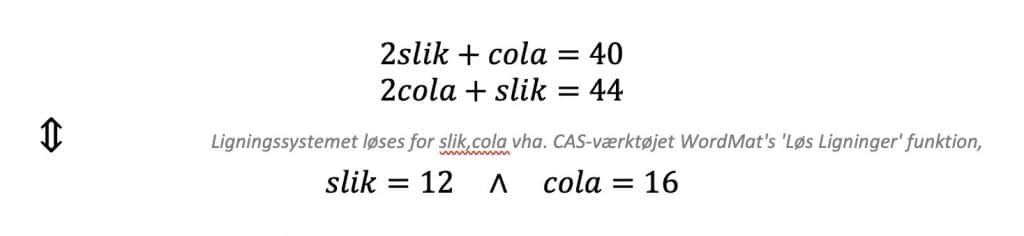
Igen fandt vi, at en cola koster 16 kr. og en pose slik 12 kr.

Symbolsk – løst ved at isolere en ubekendt

Jeg bruger s for slik og c for cola.

2s + c = 40
2c + s = 44

Jeg bruger første ligning til at isolere c:

2s + c = 40
c = 40 – 2s

Så indsætter jeg dette udtryk for c i den anden ligning:

2(40 – 2s) + s = 44

Nu har jeg en ligning med én ubekendt, den reducerer jeg først:

80 – 4s + s = 44
80 – 3s = 44

Så løser jeg ligningen ved at trække 80 fra på begge sider:

-3s = 44 – 80
-3s = -36

Så dividerer jeg på begge sider med -3:

s = -36 : (-3)

Og finder                                                  

s = 12

Nu kan værdien for s bruges i én af ligningerne til at finde c, jeg bruger den første ligning

2s + c = 40

Indsætter s=12

2 * 12 + c = 40

Endelig løser jeg denne ligning, der kun har én ubekendt, nemlig c:

c = 40 – 24
c = 16

Igen fandt vi en cola koster 16 kr. og en pose slik 12 kr.

Lav selv ligningssystemer

Man kan også arbejde med at lade eleverne lave ligningssystemer selv. Det kan gøres konkret med centicubes.

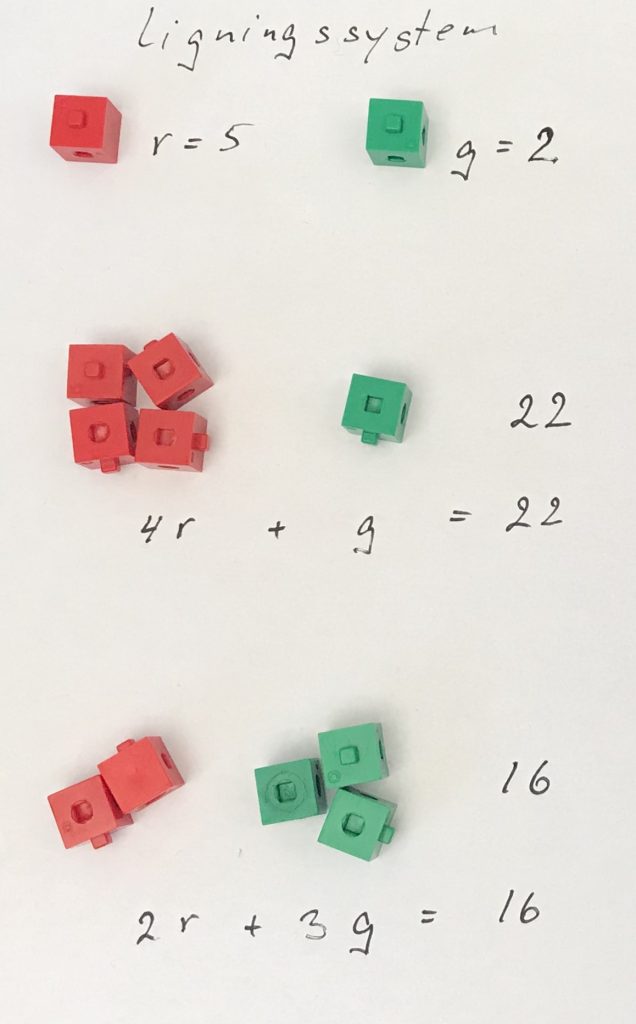
Hvis man vil lave ligningssystemer med to ubekendte tager man centicubes i to farver, fx røde og grønne centicubes. Man beslutter så hvad hhv en rød og en grøn centicube skal være værd. Fx kan en rød være 5 værd og grøn være 2 værd. Man beslutter sig altså for en løsning, inden man laver ligningssystemet.

Så kan man bygge sit ligningssystem op ved at tage forskellige portioner af de røde og grønne centicubes, og regne ud hvad de forskellige portioner er værd. For eksempel er en portion med 4 røde og 1 grøn 4 * 5 + 2 = 22 værd og en anden portion med 2 røde og 3 grønne er 2 * 5 + 3 * 2 = 16 værd. Nu har vi vores ligningssystem:

4r + g = 22
2r + 3g = 16

Eleverne kan arbejde i par og bytte ligningssystemer med hinanden.

Når eleverne har fået sig nogle erfaringer med at bygge sådanne ligningssystemer kan man få dem til at overveje følgende spørgsmål:

1. Hvorfor kan man nogle gange ikke løse et ligningssystem?
2. Hvor mange ligninger skal man mindst have i sit ligningssystem, hvis man har 2 ubekendte? Eller 3 ubekendte?

Der er flere muligheder for, hvorfor man ikke kan finde én løsning til et ligningssystem. Ret ofte vil man opleve, at det ser ud til at der er to forskellige ligninger, men når man ser nærmere på det, så er de to ligninger ens, den ene er bare den andet ganget op. For eksempel er de to ligninger nedenfor ens, på den måde at de har de samme løsninger, da den nederste ligning er den øverste ganget med 2.

4r + g = 22
8r + 2g = 44

Man kan også opleve at man har for få ligninger til at kunne finde en løsning. Og det er svaret på spørgsmål 2. Man skal have samme antal ligninger, som man har ubekendte. Har man for få ligninger er der i virkeligheden uendelig mange løsninger. Har man for eksempel kun en ligning som 4r + g = 22 så har den løsningen r = 5 og g = 2, men den har også løsningen r = 1 og g = 18, den har nemlig alle de løsninger der ligger på linjen givet ved 4r + g = 22 eller udtrykt som vi kender det: y = -4x + 22.

På den måde vi opbygger ligningssystemer her skulle alle ligningssystemer have løsninger, når bare de, der opbygger ligningssystemet, regner rigtigt. I andre sammenhænge kan man nemt opleve, at et ligningssystem ingen løsninger har.

Ligningssystemerne kan laves større, hvis man bruger flere farver og flere ligninger.

De ligningssystemer man skaber på denne måde har kun positive, heltallige koefficienter. Og der findes naturligvis mange andre typer ligningsystemer i denne verden.

Vi har lavet en lille video, hvor Pernille på mindre end 3 minutter demonstrerer hvordan man kan lave sine egne ligningssystemer og løse dem.https://www.youtube.com/embed/MXRfC_1xM8Y?feature=oembed

I vores bog “Gode grublere og sikre strategier” har vi blandt meget andet en masse sjove eksempler på ligningsløsning i forbindelse med grublere.