Problemløsning / Lovport
Kapitel 1 af bogen “Gode grublere og sikre strategier”
Bogen kan købes i vores online-butik.
Formålet med denne bog er at give en hjælp til undervisning i det svære område problemløsning. Matematikundervisning har generelt stort fokus på færdigheder og begreber. Arbejdet med matematiske strategier er også særdeles vigtigt – og fokus for denne bog.
Problemløsningskompetencen er en central matematisk kompetence. En kompetence som ikke kun kan bruges til klassiske matematiske problemer, men også til problemer af mere sammensat og kompleks natur.
Det er svært at få fat i, hvad det egentlig er vi gør, når vi løser problemer. “Jeg gør det bare”, “Det er forskelligt fra gang til gang”, og “Det har jeg egentlig ikke tænkt over” er typiske svar fra folk, der har arbejdet med matematiske problemer. Det illustrerer, at problemløseren bliver optaget af selve problemet, mens metatænkningen – refleksionen over, hvordan man egentlig gør – tager man sig ikke tid til.
I denne bog ser vi på begge dele. I dette kapitel gennemgås en række problemløsningsstrategier fra de meget overordnede, som vi kalder vaner, over en generel metode til problemløsning, til en række forskellige strategier man kan vælge mellem i arbejdet med et konkret problem. Derefter gennemarbejdes 25 klassiske problemer med brug af en række forskellige problemløsningsstrategier, så man kan opleve dem i aktion.
Man må endelig ikke fristes til at tro, at arbejdet med problemløsningsstrategier kun er for dygtige elever. Tværtimod. Elever, som finder matematik vanskeligt, mangler i særlig høj grad disse generelle værktøjer. Og man lærer kun noget ved at prøve det, også selv om det er svært.
Hvad er en grubler
Vi har kaldt bogen “Gode grublere og sikre strategier”. De problemer, vi præsenterer i bogen, skal næsten alle gruble over. Det tænder de fleste, men nogle elever bliver utrygge ved manglen på konkrete løsningsmetoder.
Når man arbejder med problemerne, befinder man sig altså i en problemløsningssituation og ikke i en opgavesituation, hvor det bare handler om at anvende en bestemt færdighed, og så er den opgave løst.
I min bog “Matematik for alle – håndbog i matematikundervisning” beskriver jeg aktiviteter i matematikundervisningen i forhold til graden af åbenhed, inddragelse af virkelighed og problemløsning. Det er vigtigt at bevæge sig rundt blandt disse aktiviteter og komme et stykke ud af alle tre akser, da virkeligheden udenfor skolen ligger langt ude af alle tre akser.
Grublere ligger højt oppe ad problemløsningsaksen. Grublere er typisk ikke ret langt ude på åbenhedsaksen. Og selvom grublere oftest er givet i en kontekst, så er den kontekst sjældent så virkelig, at man kan drage nytte af sine erfaringer fra virkeligheden.
Aktiviteter, hvor eleverne bevæger sig i ukendt territorium, for eksempel at arbejde med problemløsning, kræver støtte fra læreren. Læreren skal være tydelig omkring sine forventninger til eleverne. Ingen elever forventes at kunne løse grubleren umiddelbart. Formålet med arbejdet er, at alle skal prøve at arbejde med problemløsningsstrategier, hvor selve det at finde ud af, hvad man skal gøre, er pointen. Tit kan det også støtte den enkelte elev at tage fælles samtaler med elever, der arbejder med samme problem, hvor elevernes samlede viden er med til at løfte hver enkelt elev videre.
LOVPORT – en metode til problemløsning
Der findes en række forskellige metoder til problemløsning. Jeg har med succes arbejdet med nedenstående, som er inspireret af bogen “Teaching Mathematics to Middle School Students with Learning Difficulties”.
Eleverne skal gennemgå nedenstående syv skridt, når de løser problemer.
L for “Læs”
Eleven skal læse teksten grundigt. Gerne læse den højt for en kammerat. Det centrale i dette skridt er, at man får taget fat i ord, man ikke forstår, får spurgt til dem, slået dem op eller lignende, så man er sikker på, at man forstår alle ord. Man skal være opmærksom på, om der er ord, der kan have flere betydninger, og hvor den matematiske betydning kan være anderledes end hverdagsbetydningen. Der kan også være ord, der er særlig vigtige, og som giver et hint til hvilken problemløsningsstrategi, man senere skal vælge.
Man kan strege nøgleordene i teksten under, så man på den måde får tydelig gjort det centrale.
O for “Omformuler”
Eleven skal nu omformulere teksten med sine egne ord. Hvis elever arbejder sammen i makkerpar, kan den ene læse højt, de kan sammen gå teksten igennem som beskrevet ovenfor, og den anden kan så omformulere teksten med sine egne ord. I dette skridt vil problemets staffage, historien, forhåbentlig blive nedtonet, hvorved det matematiske problem kommer til at stå tydeligere.
Efter læsning og omformulering har eleven forstået problemet i alle dets detaljer. Næste punkt – visualiser – hjælper eleven til at forstå problemet i dets helhed.
V for “Visualiser”
Eleven skal nu arbejde med at få dannet et mentalt billede af problemet – et billede, der griber hele problemet på en gang, og som kan rummes i elevens hoved. Mentale billeder kan hjælpes på vej ved at tegne et fysisk billede af problemet eller bygge problemet med konkrete materialer.
De tre første punkter (LOV) skal tilsammen give forståelsen af problemet. Det er helt i orden at bevæge sig lidt mellem skridtene frem og tilbage, men det er ikke i orden at undlade nogle af skridtene.
Ofte oplever eleverne, at hvis de har arbejdet grundigt med de tre første skridt, så falder problemløsningen så let, at de næste punkter håndteres nemt.
P for “Planlæg”
I planlægningsskridtet skal man til at se på de ni sikre strategier. Er der en af dem, der virker oplagt at tage fat på? Skal man have gang i to problemløsningsstrategier? Eller …?
I nogle situationer kan man umiddelbart se hvilke færdigheder, der skal bruges for at løse problemet, og så er valget af problemløsningsstrategi overstået næsten før, det er startet.
Planlægningen er ofte det sværeste skridt at huske, for når nu problemet er forstået, vil eleverne bare til at løse det, og springer direkte til “regn”. Hvis det går galt, skal eleverne tit tilbage til planlægningen.
O for “Overslag”
I dette skridt skal man give et gæt på løsningen eller formulere en hypotese om løsningen. Eller i hvert tilfælde en hypotese om i hvilken retning man forventer en løsning. I problemer, der har mere med virkeligheden at gøre, end grublere har, kan man her inddrage sine erfaringer fra hverdagen eller fra andre fag, men i grublere har man ikke så meget virkelighed at trække på, og ens gæt må baseres på erfaringer fra andre grublere eller lignende problemer.
R for “Regn”
Nu kan man endelig få lov til at udfører sin plan fra punkt P. I mange tilfælde skal man regne, men i andre tilfælde betyder ens plan, at man skal tegne, bygge, dramatisere eller noget helt andet.
Det er her, det afgørende slag med problemet står. Ofte opdager man nu, at man egentlig ikke har forstået problemet ordentligt, og man må tilbage til de første tre skridt igen. Hvorefter man også bliver nødt til at genoverveje planlægningen og genoverveje sit overslag.
Dette skridt kan godt kræve nogle ture rundt i de forudgående skridt.
T for “Tjek”
Selvom man er nået til en løsning, er man ikke helt færdig. Først skal man tjekke om løsningen passer med ens gæt. Stemmer gæt og løsning rimeligt sammen, ja så har man grund til at tro, at man er færdig. Stemmer de to ikke passende overens, må man til at overveje, om gættet var skævt, eller om man har løst problemet forkert. Og kan så spole baglæns og vurdere, om man har regnet/udført planen rigtigt og endelig genoverveje, om man egentlig har forstået problemet korrekt.
Og til allersidst kan man kontrollere, om løsningen er korrekt ved at prøve/regne/tegne efter.
Værdifulde vaner
Nogle strategier er så overordnede og nyttige i alt arbejde med matematik, at vi har valgt at kalde dem værdifulde vaner.
Vær systematisk
At være systematisk betyder, at man gennemgår mulighederne på en struktureret måde. Det er en god vane til megen problemløsning. Når man er systematisk, undgår man at prøve de samme løsningsmuligheder flere gange, og man er sikker på, at man kommer igennem alle relevante muligheder. Derudover betyder den systematiske tilgang, at man bedre kan overskue sine resultater undervejs, og eventuelt opdage mønstre som gør, at man kan komme løsningen nærmere hurtigere.
Strategierne “gæt og prøv efter” og “udtøm alle muligheder” baserer sig kraftigt på en god systematik.
God systematik kan ofte støttes af tabeller, skemaer eller tælletræer.
Brug notation
Notation er særlige symboler eller forkortelser. Brug af notation øger overskueligheden af mange problemer, fordi kompakt opskrivning helt konkret gør beskrivelsen af problemet mindre.
Notation er for eksempel brug af bogstaver i stedet for navne, brug af bogstaver i stedet for tal og brug af symboler. Man må gerne selv opfinde symbolerne, men man kan også bruge nogle af dem, der er opstået blandt videnskabsfolk gennem mange hundrede år. God notation kommer ikke af sig selv, men er noget man skal tænke over og prøve sig frem med. For eksempel skal man nødigt anvende samme bogstav for forskellige ting, og samtidig skal notationen være nem at huske.
Undersøg forskellige synsvinkler
Vanskelige problemer kan løses op ved at afprøve mange forskellige ideer til problemløsningen. Gode ideer opstår blandt andet ved at udnytte kendt viden i andre sammenhænge og ved at sammensætte metoder og viden fra forskellige fag.
Nogle gange kan man godt knokle sig igennem et problem ved hårdt arbejde, men havde man brugt mere tid på at tænke over alternative tilgange, havde der måske været en nemmere løsningsmetode. Andre problemer kan ikke løses med traditionelle metoder, men kræver en kreativ ide.
Kreativiteten kan støttes ved at lave mange forskellige repræsentationer af problemet: Forskellige formuleringer, forskellige former for notation, fysisk repræsentation eller dramatisering. Kun fantasien og kreativiteten sætter grænser. Kreativiteten kan blive hæmmet af vanetænkning og begrænsninger, som traditionelt findes.
Sikre strategier
Under planlægningsdelen af LOVPORT skal man vælge hvilke(n) strategi(er) man kan løse problemet med. Nedenfor beskrives ni strategier, som kan bruges i utallige situationer.
Reducer problemet
Start med at reducere problemet til et nemmere problem, og løs dette problem for derigennem at få ideer til, hvordan man kan løse det oprindelige problem. Mange problemer kan reduceres ved at bruge nemmere tal. Nemmere tal kan være små tal, tier-potenser (10, 100, …) eller tal, som de øvrige går op i eller er delelig med. Andre problemer kan reduceres ved at reducere antallet af skridt.
Optrævling
Man starter bagfra og trævler problemet op ved at tage et skridt ad gangen og bruge delresultatet til næste skridt. Mange problemer, der er baseret på rekursion, altså det at gentage en procedure på sig selv, kan løses med optrævling.

Luk åbne problemer
Hvis der tilsyneladende mangler oplysninger, eller problemet er åbent eller generelt, kan man ofte tillade sig selv at finde på nogle af de manglende oplysninger. Derved lukker man problemet og gør det muligt at løse.
Når man selv kan finde på de manglende oplysninger, bør de vælges så udregningerne bliver nemme.
Opstil og løs ligninger
Problemers oplysninger og sammenhænge kan ofte samles i en eller flere ligninger. Man skal finde ud af, hvilke ubekendte man har, og hvordan de hænger sammen. Når ligningerne er stillet op, kan de løses med elektroniske hjælpemidler eller traditionelle ligningsløsningsmetoder.

Gæt og prøv efter
Man kan gætte på en løsning, og prøve om den giver den korrekte løsning. Nogle gange kan man gætte mange gange, og kvalificere sine gæt efterhånden som man indser, hvordan gættene skal justeres.
Man kan også starte problemløsningen med at gætte. Ved gæt og efterprøvning øges forståelsen af problemet. Når man kender problemet bedre, kan man skifte til mere direkte løsningsstrategier.

Vær konkret
Nogle problemer forstås bedre, hvis man dramatiserer problemet som et lille skuespil med aktører, replikker og konkrete materialer. Andre gange kan brug af konkrete materialer eller tegning hjælpe problemløsningen.
Nogle gange kan en bunke småsten være nyttige. Andre gange er det en fordel at have farver på, og så er centicubes bedre. Og andre gange er det en fordel at kunne vende materialet, og så er dominobrikker, spillekort eller tændstikker bedre.

Brug logik
I mange problemer skal man bruge den helt basale logiske regel, at et udsagn enten er sandt eller falsk – ikke begge dele. Det lyder banalt, men det er ikke altid lige let at gennemskue, om man kan udelukke det ene og dermed konkludere det andet.

Udtøm alle muligheder
Hvis problemet har et overskueligt antal løsningsmuligheder kan man finde alle de mulige løsninger og undersøge dem en for en.
Det kræver systematik og god orden at sikre sig, at man faktisk har alle de mulige løsninger med, inden man giver sig til at undersøge hver enkelt. Med regneark kan man håndtere selv ret store mængder mulige løsninger.

Et skridt ad gangen
I mange klassiske matematiske problemer er det muligt at starte forfra med startbetingelserne og så ved hjælp af matematik og logik deducere sig stille og roligt gennem problemet skridt for skridt: Hvis det her gælder, så medfører det, at det her gælder og så videre.

Differentieringsmuligheder
Som lærer er muligheden for at kunne lave undervisningsdifferentiering altid vigtig. Undervisningsdifferentiering kan blandt andet praktiseres ved at kunne lave flere variationer over det samme problem, så elever kan udfordres på forskellige niveauer.
Lettere variationer
Læreren kan lave lettere variationer af et problem. Læreren kan vælge at give denne lettere variant i stedet for den originale grubler til de elever, som man ved har behov for en mere tilgængelig version.
Man kan lave lettere varianter af et problem ved at bruge nemmere tal i problemet, reducere antallet af skridt, give flere oplysninger fra starten og/eller lukke de eventuelle åbninger, der er i problemet.
Løft af problemet
Der er også elever, der skal have ekstra udfordringer, efter de har løst det originale problem. Jeg kalder det at give problemet et matematisk løft.
Generelt kan man give problemer et matematisk løft ved at indsætte vanskeligere tal i problemet, tilføje yderligere skridt og/eller åbne problemet ved at fjerne oplysninger. Man kan også bede eleven om at finde andre løsninger eller finde en generel løsning på problemet.
Endelig kan man også give bolden op til elevens egne undersøgelser, hvor eleven selv rejser og besvarer spørgsmål. Det er det mest krævende løft, da eleven selv skal arbejde videre helt åbent og selv skal lære at lave de matematiske løft.
Eleverne skal huske på, at de selv skal svare på de nye spørgsmål, de stiller sig. Det er ikke nok at formulere nye spørgsmål eller forklare, hvordan de kan løses. Ofte er løsningen ikke så nem, som man forestiller sig.
Grublere i klassen
Det er en god ide at introducere LOVPORT før eleverne går i gang med at arbejde med grublerne. LOVPORT kan med fordel introduceres i forbindelse med løsning af tekstopgaver.
LOVPORT er velegnet til samarbejde (to og to eller i lidt større grupper), hvor eleverne skiftes til at læse højt og omformulere og derefter samarbejder om resten af punkterne. Når eleverne husker hinanden på, hvor de er nået til i LOVPORT, mindskes risikoen for at springe skridt over.
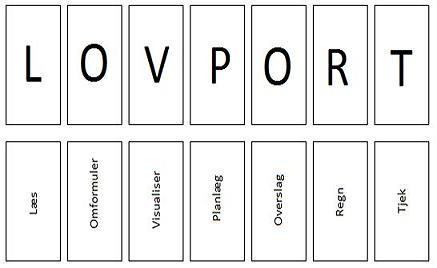
Man kan helt konkret udstyre hvert hold elever med et sæt LOVPORT brikker. Det er syv stykker karton på ca. 6 cm x 10 cm, hvor der på den ene side står bogstavet (fx L) og på den anden side står det ord, bogstavet står for (fx Læs). Eleverne skal lægge bogstavet op foran sig på bordet, når de arbejder med det aktuelle skridt. Efterhånden kommer der mere og mere af LOVPORT frem, og læreren kan på den måde se, hvor langt eleverne er. Man kan introducere de ni sikre problemløsningsstrategier, inden eleverne går i gang med at arbejde med grublerne. Det er en god ide at hænge skilte med de ni problemløsningsstrategier op i klassen, så eleverne konstant kan se på strategierne og er bevidst om dem. Det er også en god ide, at lade eleverne føre de ni forskellige strategier ind i deres personlige formelsamling, hvor de kan beskrive strategierne med deres egne ord og føje eksempler til, når de møder dem.
Man kan også undlade at gennemgå strategierne på forhånd og først samle op på elevernes egne problemløsningsstrategier for derefter supplere med de strategier, som eleverne ikke har brugt. Uanset om strategierne gennemgås på forhånd eller ej, er det vigtigt at samle op på problemløsningsstrategierne efter arbejdet med grublerne, det er netop det, der er pointen med arbejdet med grublere.
Selve grublerne kan præsenteres fælles, eventuelt på elektronisk whiteboard, hvorefter eleverne arbejder med grubleren. Efterhånden som eleverne bliver færdige, udfordres de hurtigste med matematiske løft. Når alle er nået gennem grubleren trækkes lod om, hvem der starter med at gennemgå sin måde at løse grubleren, og flere forskellige problemløsningsstrategier vises på tavlen og diskuteres. Husk eleverne på, at pointen er de forskellige problemløsningsstrategier i højere grad end selve løsningen.
Man kan også vælge, at eleverne arbejder med forskellige grublere. Eleverne er på denne måde mindre pressede af den konkurrencestemning, der kan opstå, når alle arbejder med den samme grubler. Opsamlingen af forskellige problemløsningsstrategier er vanskeligere her, da det kan være vanskeligt for læreren at have overblik over, hvornår alle har været igennem den samme grubler. Et fælles oversigtsskema kan lette dette overblik.
——–
Mange tak til Inge Toft, Borremose Efterskole for illustrationer.





