Matematisk kagedeling
Denne artikel handler om at dele. Det er en forunderlig blanding af matematik og psykologi, da det handler om måder at dele på, som føles retfærdigt for de der deler, men ikke nødvendigvis er delt lige – sådan rent matematisk.
Tænk på det som at dele et stykke af en kagemand. På en kagemand er der mange ting, der spiller ind ud over det eksakte areal eller rumfang af kagestykket. For eksempel bliver et stykke mere attraktivt, hvis ens yndlingsslik er på det, eller hvis der er netop den mængde glasur eller kant, som man selv bedst kan lide.
Dette handler altså om metoder til at dele noget, hvor det ikke bare er så nemt at måle det op, dividere og så dele ud.
Når to skal dele
Først ser vi på den situation, hvor kun to personer skal dele et stykke kagemand. Her tror jeg faktisk, de fleste af os kender metoden: den ene deler og den anden vælger først. Denne metode er retfærdig, fordi begge parter føler, at de har fået en del, der er det halve eller lidt mere værd end hele stykket. Den er også misundelsesfri, fordi begge parter føler sig overbevist om, at den anden ikke har fået et stykke, som de hellere ville have haft.
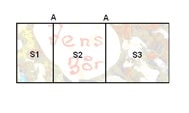
Med bogstaver og lidt matematik ser det således ud: A (Anne) deler kagen i to stykker S1 og S2, som har lige stor værdi for Anne. A synes altså at S1=S2=1/2 af kagens værdi for hende. B (Bo) vælger et af stykkerne, for eksempel S1. Det gør Bo fordi han synes at S1>S2 og dermed er S1>1/2 af kagens værdi for ham. A får så S2.
A er tilfreds, da hun får noget, hun synes er en halv værd, og hun er heller ikke bekymret over, om B får noget hun hellere ville have haft, da begge stykker er lige meget værd for hende.
B er tilfreds, da han får noget, han synes er en halv eller mere værd. B får et stykke, han synes, har den samme eller større værdi, end det stykke A får.
Når tre skal dele
Når der er mere end to til at dele et stykke kage, er det noget mere besværligt. Jeg vil beskrive to metoder, der er retfærdige, i den forstand at alle tre parter får et stykke, som de selv vurderer til at være 1/3 eller mere værd for dem. De to metoder er dog ikke misundelsesfrie, da man risikerer, at der er en eller flere, der føler, at andre har fået et stykke, de hellere selv ville have haft. Til sidst beskriver jeg en metode, som både er retfærdig og misundelsesfri.
Metode 1: Del og del igen
A, B og C skal dele et stykke kagemand. Det gør man ved at lade A og B dele kagen først ved metoden ovenfor: den ene deler og den anden vælger. Så kommer C og beder både A og B om at dele hver sit stykke i tre lige store dele. Så tager C et stykke fra hver af A og B, C tager selvfølgelig de stykker, som han synes bedst om.
A føler at hun har fået 2/3*1/2=1/3
B føler han har fået 2/3*1/2=1/3
C føler at han har fået 1/3 af to stykker som tilsammen giver det hele, dvs. 1/3*1=1/3
Men metoden er ikke misundelsesfri. Fx kan A godt risikere at synes, B’s deling af stykket er helt åndsvagt uretfærdigt, så C derfra kan tage et stykke, som i A’s øjne er meget mere værd end 1/3 af B’s stykke, så C på denne måde ender op med noget, som i A’s øjne er mere end 1/3 værd alt i alt, og altså mere værd end A’s eget stykke. Man kunne oven i købet forestille sig at B og C har rottet sig sammen, så B er tilfreds med to mikrosmå stykker i anden omgang, så C får næsten hele B’s stykke.
Metode 2: Den flyvende kniv
Denne metode kræver en rolig hånd og et godt øre af en uvildig person (for eksempel en mor), der ikke selv deltager i kagespiseriet. Den uvildige person skal føre en kniv langsom henover kagestykket, og være god til at stoppe kniven præcis, når en af de tre kagespisere råber “stop”. Ideen er altså, at de tre kagespisere følger kniven og råber stop, når de synes at kniven har afgrænset 1/3 af kagen. Lad os sige, at A er den der først råber stop, og A får således første stykke, og forlader kagedelingen. Den uvildige person fortsætter med at flytte kniven langsomt henover stykket, og den af de to resterende kagespisere, der først råber stop, får det næste stykke. Lad os sige, det er B, der går med det næste stykke. Den af de tre kagespisere, der ikke råbte stop, eller bare ikke nåede det før de andre, ender med det sidste stykke, i dette tilfælde er det altså C.
A må få noget, hun vurderer til 1/3, ellers ville hun jo ikke have råbt stop. B må ligeledes få noget han vurderer til 1/3, ellers ville han jo ikke have råbt stop, da han gjorde det. C må endelig også føle, at han får noget, der er 1/3, ellers ville han jo have råbt stop på et tidligere tidspunkt.
Men metoden er ikke misundelsesfri. Fx kan A godt synes, at B og C gambler lidt rigeligt, hvis begge venter med at råbe stop i håb om, at den anden trods alt er langsommere. Det giver resultatet, at fx B ender som vinder og får et kæmpestykke i A’s øjne. C føler sig egentlig ikke snydt på trods af, at han i A’s øjne kun får et lille stykke, da han jo “spillede med” og vidste, at han risikerede at tabe til B.
Metode 3: Indviklet – men retfærdig og misundelsesfri
A, B og C skal igen dele et stykke kagemand. A deler stykket i tre stykker S1, S2 og S3.
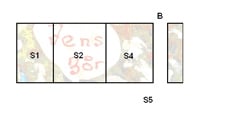
B får nu lov til at justere et af de tre stykker, hvis han synes, der er et stykke, der er større end de to andre. B får således lov til at skære et stykke af et af stykkerne, så han synes, at der nu er to lige gode stykker og et, der er dårligere, eller så han synes, der er tre lige gode stykker. Der er nu stykkerne S1, S2, S4 og S5
De tre stykker S1, S2 og S4 deles nu ud til A, B og C på følgende måde:
- C vælger først.
- B vælger dernæst. Hvis C ikke vælger S4, som er det justerede stykke, så skal B vælge dette stykke. Han synes jo det er det bedste. Vi kalder den af B eller C, der får det justerede stykke (S4) for J, og den der får det ikke-justerede stykke for IJ
- A får det sidste stykke, og A synes, det er lige så godt som de andre – det var jo A som lavede første deling
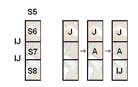
Stykkerne er nu fordelt på en af disse to måder:
Dernæst skal S5 deles i tre stykker. Det skal IJ gøre, da han nu også skal tage ansvar for en deling. S5 deles i stykkerne S6, S7 og S8.
Så skal de tre stykker S6, S7 og S8 deles ud til A, B og C. Det gøres på følgende måde:
- J vælger først.
- Dernæst vælger A.
- Og IJ får det sidste stykke. Da han har lavet delingen, synes han jo, at alle tre stykker er lige gode.
Jeg lovede at denne deling er både retfærdig og misundelsesfri. For at undersøge det, skal vi regne lidt:
Alle tre er enige om:
S1+S2+S3=1
S3=S4+S5
S5=S6+S7+S8
I situationen hvor B fik det justerede stykke (B er J), ender vi for eksempel med at
A får S1+S7
B får S4+S6
C får S2+S8
A vurderer kagestykkerne således:
S1=S2=S3=1/3 (A lavede jo den første deling)
S1=S2=S3=S4+S5=S4+S6+S7+S8 Dvs. S1>S4+S6
S7³S8 (A valgte S7 frem for S8)
A synes hun får mere end 1/3 af hele kagen, da hun synes S1=1/3.
Altså er delingen retfærdig for A.
A synes hun får mere end B, da A synes S1>S4+S6
A synes hun får mere end eller lig med C, da A synes S1=S2 og S7³S8
Altså er A ikke misundelig på hverken B eller C
B vurderer kagestykkerne således:
S4=S2³S1
S6³S7 og S6³ S8
B synes han får mere end eller lig med A, da B synes S4³S1 og S6³S7
B synes han får mere end eller lig med C, da B synes S4=S2 og S6³S8
Altså er B ikke misundelig på A eller C
B synes han får mere end eller lig med 1/3 af hele kagen, da han synes han får mere end eller lig med de to andre.
Altså er delingen retfærdig for B
C vurderer kagestykkerne således:
S2³S1 og S2³S4
S6=S7=S8 (da C delte S5 i disse 3 stykker)
C synes han får mere end eller lig med A, da C synes S2³S1 og S8=S7
C synes han får mere end eller lig med B, da C synes S2³S4 og S8=S6
Altså er C ikke misundelig på A eller B
C synes han får mere end eller lig med 1/3 af hele kagen, da han synes han får mere end eller lig med de to andre.
Altså er delingen retfærdig for C
Hvordan deler man, hvis man er flere end tre?
Metode 2 (Den flyvende kniv) er nem at udvide til flere personer. Man kan dog forestille sig, at det bliver ret svært i praksis at høre forskel på, hvem der råber først, men så må man trække lod blandt de, der råber samtidig. Metoden er som sagt ikke misundelsesfri, og den lægger i høj grad op til gambling.
Metode 1 kan også udvides til flere personer. Ved fire personer gøres først som ovenfor med de tre første. Disse tre har nu hver to stykker kage, der er i alt seks stykker kage. De tre deler nu hver af deres to stykker i fire stykker. Det giver i alt seks bunker med fire stykker i hver, i alt 24 stykker kage. Den fjerde person går nu rundt og vælger sit favoritstykke i hver af de seks bunker. Det giver seks stykker kage til hver.
Denne metode giver hurtigt urimelig mange og urimelig små stykker kage, og metoden er som tidligere nævnt ikke misundelsesfri.
Metode 3 kan ikke umiddelbart udvides til flere personer. Til mange mennesker findes der dog kagedelingsmetoder, der både er retfærdige og misundelsesfrie – men de er ret komplicerede!
Opgaver
Opgave 1
Ved metode 3 gennemregnes kun situationen hvor B er J. Hvordan er de tilsvarende argumenter i den situation, hvor B er IJ?
I den situation ender vi for eksempel med at
A får S1+S7
B får S2+S8
C får S4+S6
Opgave 2
Hvis nu B synes, der ikke er et stykke, der er større end de to andre, så vælger B altså, at han ikke vil skære noget af nogen af stykkerne, så er S5=0. Argumenter for, at også denne deling er retfærdig og misundelsesfri
Svar på opgave 1
A synes:
S1=S2=S3=1/3
S1=S2=S3=S4+S5=S4+S6+S7+S8
Dvs. S1>S4+S6
S7³S8
A synes hun får mere end 1/3 af hele kagen, da hun synes S1=1/3
A synes hun får mere end eller lig med B, da A synes S1=S2 og S7³S8
A synes hun får mere end C, da A synes S1>S4+S6
B synes:
S3>S2³S1
S4=S2³S1
S6=S7=S8
B synes han får mere end eller lig med A, da B synes S2³S1 og S8=S7
B synes han får lig med C, da B synes S2=S4 og S8³S6
B synes han får mere end eller lig med 1/3 af hele kagen, da han synes han får mere end eller lig med de to andre.
C synes:
S4³ S2 og S4³S1
S6³ S7 og S6³S8
C synes han får mere end eller lig med A, da C synes S4³S1 og S6³S7
C synes han får mere end eller lig med B, da C synes S4³S2 og S6³ S8
C synes han får mere end eller lig med 1/3 af hele kagen, da han synes han får mere end eller lig med de to andre.
Svar på opgave 2
Alle tre er enige om:
S1+S2+S3=1
S3=S4+S5=S4
S5=S6+S7+S8=0
Der er kun to væsensforskellige delinger.
Deling 1:
A får S1
B får S4=S3
C får S2
A synes:
S1=S2=S3=1/3
A synes hun får 1/3 af hele kagen, da hun synes S1=1/3 A synes hun får det samme som B og C.
B synes:
S4=S3=S2³S1
B synes han får mere end eller lig med A, da B synes S4³S1
B synes han får lig med C, da B synes S3=S4=S2
B synes han får mere end eller lig med 1/3 af hele kagen, da han synes han får mere end eller lig med de to andre.
C synes:
S2³ S1 og S2³S4
C synes han får mere end eller lig med A, da C synes S2³S1
C synes han får mere end eller lig med B, da C synes S2³S4=S3
C synes han får mere end eller lig med 1/3 af hele kagen, da han synes han får mere end eller lig med de to andre.
Deling 2
A får S1
B får S2
C får S4=S3
A synes:
S1=S2=S3=1/3
A synes hun får 1/3 af hele kagen, da hun synes S1=1/3
A synes hun får det samme som B og C.
B synes:
S4=S3=S2³S1
B synes han får mere end eller lig med A, da B synes S2³S1
B synes han får lig med C, da B synes S2=S4=S3
B synes han får mere end eller lig med 1/3 af hele kagen, da han synes han får mere end eller lig med de to andre.
C synes:
S4³S2 og S3=S4³S1
C synes han får mere end eller lig med A, da C synes S4³S1
C synes han får lig med B, da C synes S4=S2
C synes han får mere end eller lig med 1/3 af hele kagen, da han synes han får mere end eller lig med de to andre.