En norsk gangealgoritme
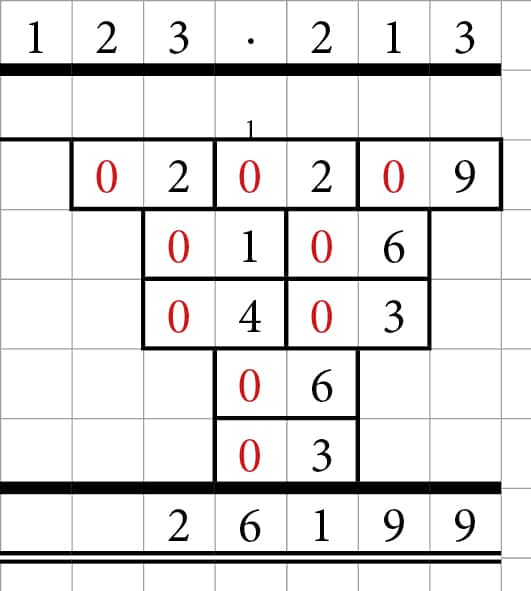
Jeg har fundet nedenstående gangealgoritme på den norske facebookgruppe ”Matematikkdidaktikk”.
Jeg synes ikke at den – ligesom alle andre ufleksible ”programmerbare” regnemetoder – bør danne grundlag for elevernes måde at regne på. MEN det er en rigtig god undersøgelse for eleverne i de ældste klasser at finde hoved og hale i algoritmen og argumentere for, hvorfor den virker.
Startskud
Vis denne udregning på tavlen, og spørg ud i klassen: Kan I finde ud af hvordan denne gangealgoritme virker?
Udvidelsen
Når eleverne har fundet ud af, hvilke resultater af hvilke gangestykker der står rundt omkring, spørger man som lærer ind til, hvad der kunne være interessant at følge op med. Det oplagte er noget a la disse spørgsmål:
1 – Hvordan virker algoritmen?
2 – Hvorfor virker algoritmen?
3 – Hvordan ligner (eller adskiller) algoritmen sig fra den måde jeg selv ganger på?
4 – Kan man gange andre 3-cifrede tal med 3-cifrede tal på samme måde?
5 – Hvordan gør man med 4-cifrede gange 4-cifrede eller 5-cifrede gange 5-cifrede tal?
6 – Hvad med gangestykker hvor tallene har forskellige antal cifre fx 4-cifret gange 3-cifret.
7 – Hvad skal man gøre, hvis der er 0’er i tallene?
8 – Er der forskel på små og store cifre i tallene?
Laboratoriet
Lad eleverne vælge undersøgelsesspørgsmål og sæt dem i gang. Helt naturligt fører nogle af spørgsmålene videre til et andet spørgsmål.
Konklusioner
Slut timen af med at få nogle konklusioner på tavlen, og lad andre elever teste konklusionerne med argumenter og modargumenter.
Mine undersøgelser – en slags svar
Ad 1 – Hvordan virker algoritmen?
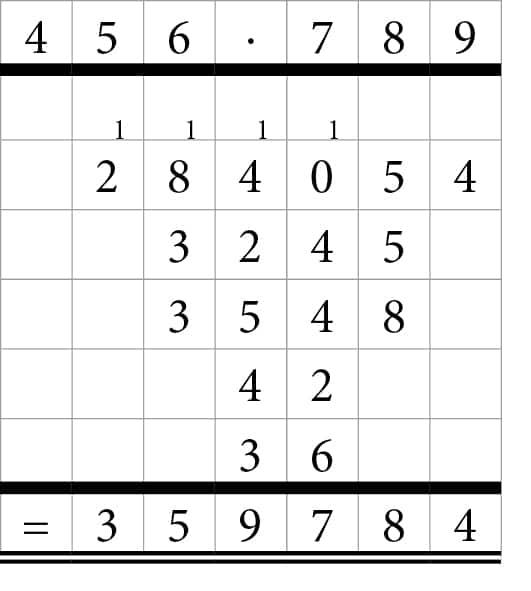
Her er de i alt 9 gangestykker med deres korrekte antal 0’er placeret. Der er lagt sammen i lodret opstilling.
Princippet i algoritmen er, at resultatet af at gange to cifre fylder to pladser. Først ganger man de cifre sammen, som står længst til venstre i de to tal (6 og 9). Resultatet står på de to pladser, yderst til højre. Man fortsætter ved at gå gennem de to tal fra højre mod venstre. Næste gang ganger man altså 5 og 8 sammen, og så ganges 4 og 7 sammen. Resultatet rykker hver gang to pladser til venstre.
Derefter fortsættes, hvor man i tallet til venstre starter næst længst til venstre. Altså udregner 5 * 9 og 4 * 8. Resultaterne rykkes også en plads til venstre.
Næste række i resultater er det samme, men omvendt: Nu er det i tallet til højre, at man starter næst længst til venstre. Altså udregner 6 * 8 og 5 * 7.
Til sidst ganges det man mangler, de to yderste og de to inderste, sammen: 6 * 7 og 4 * 9.
Ad 2 – Hvorfor virker algoritmen?
For at vurdere, hvorfor algoritmen virker, skal man overbevise sig om to ting. At de enkelte beregninger giver de korrekte værdier (og her er det jo placeringerne, altså antallet af 0’er, der er det svære) og at der bliver lavet det rigtige antal beregninger.
Beregningerne giver de rigtige værdier. Når man rykker én plads til venstre i begge tal, så bliver hver af cifrenes værdier 10 gange så store. Det betyder, at resultatet bliver 10*10=100 gange så stort som produktet af de to cifre, altså to pladser til venstre.
Når man ganger to tal hver med n cifre skal der være n*n regnestykker.
Pyramideskemaet giver det rigtige antal regnestykker. Nedenfor argumenteres visuelt for, at 5*5 pyramiden giver 25 regnestykker. 5*5 pyramiden ser fra starten således ud:
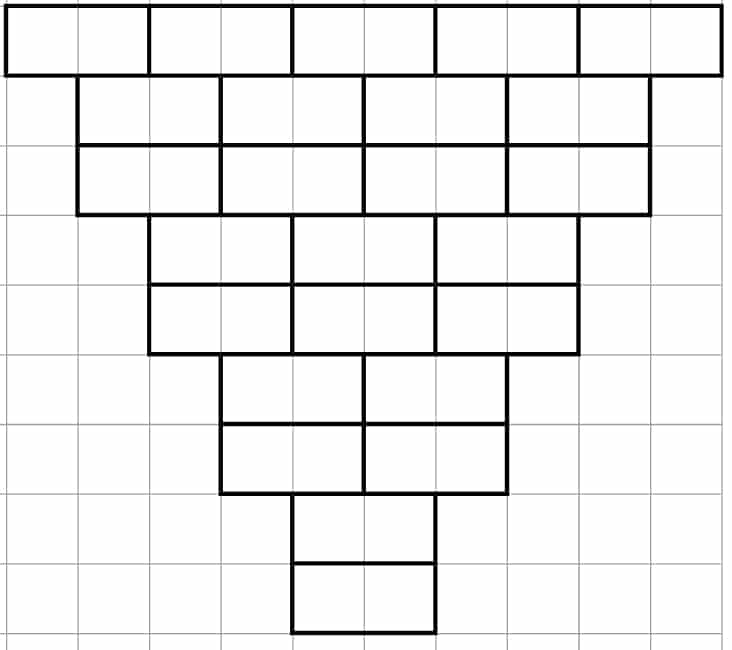
Man kan dele pyramiden i to på denne måde:
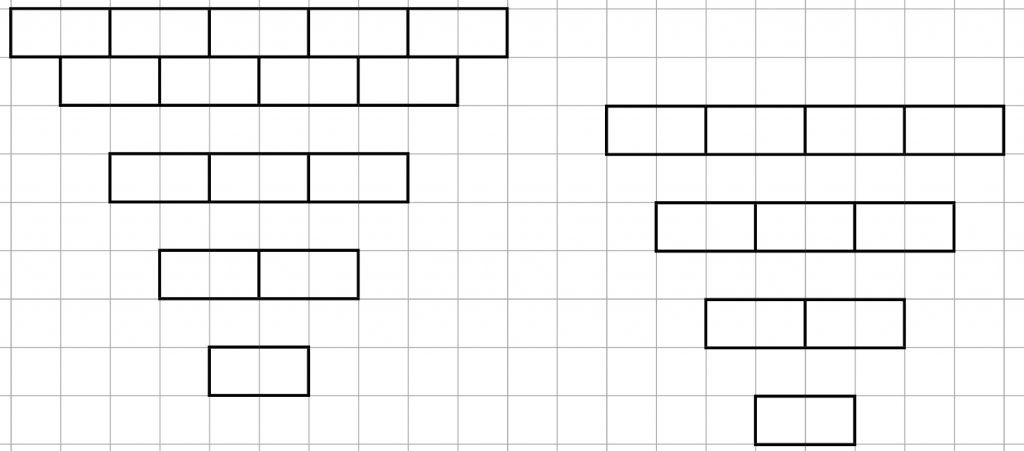
Delene samles lidt og skubbes hhv mod venstre og højre:
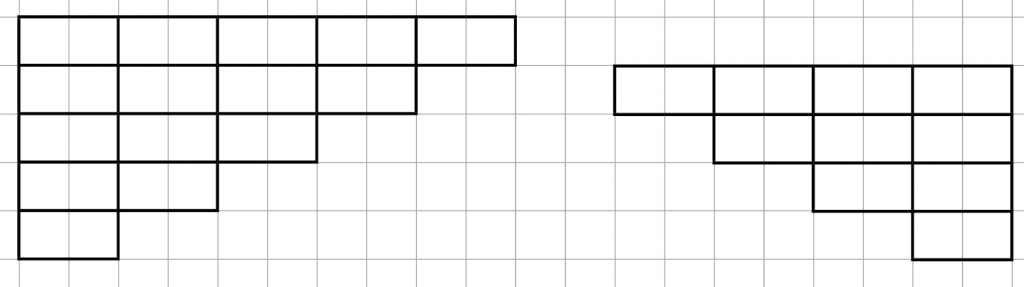
Figuren til højre spejlvendes:
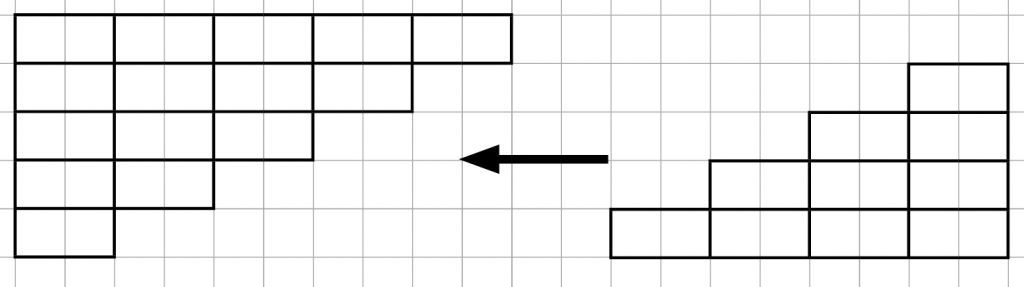
Når de to figurer skubbes sammen ses 5*5 regnestykker:
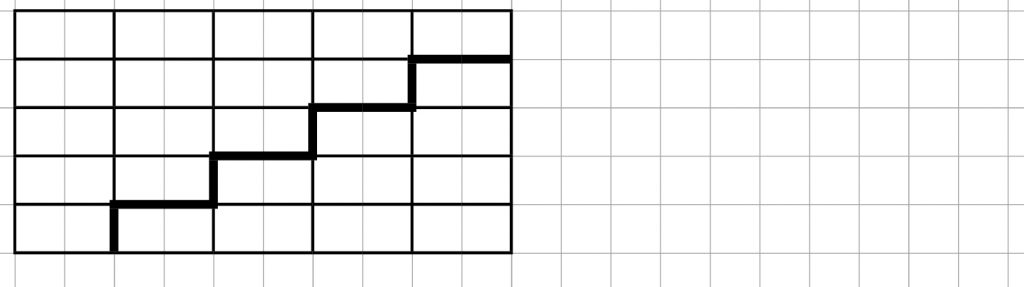
Ad 3 – Hvordan ligner algoritmen den måde jeg selv ganger på?
Jeg bruger selv arealmetoden. Hvis man ganger to tal med samme antal cifre fx n cifre og udelukkende splitter op i 1’ere, 10’ere, 100’ere og så videre får man et rektangel med n*n regnestykker.
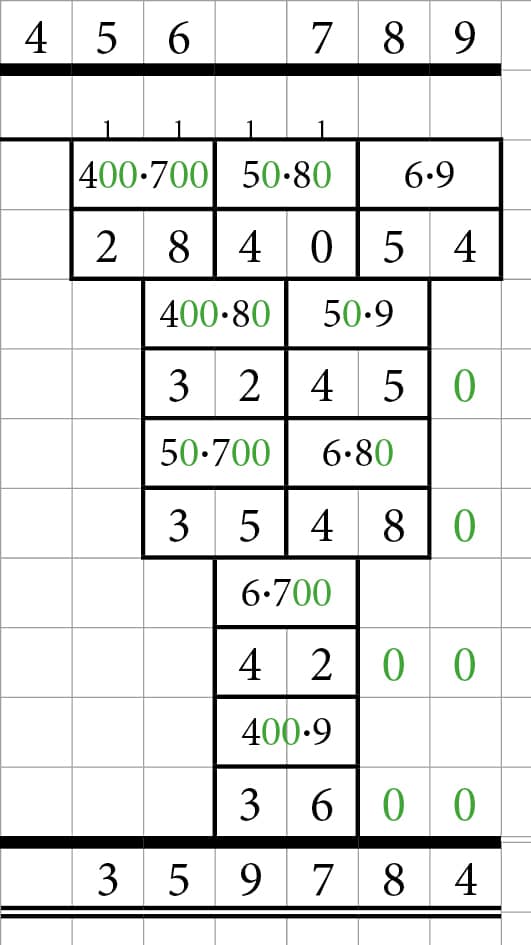
456 * 789 beregnes med arealmetoden på denne måde:

Resultaterne af de 9 gangestykker lægges sammen og giver:
280.000 + 35.000 + 32.000 + 4.200 + 4.000 + 3.600 + 480 + 450 + 54 = 359.784.
Jeg synes det er nemmere at overskue de n*n regnestykker på min måde. Særlig synes jeg det er rart at have alle 0’erne med, da jeg så har mere fornemmelse af størrelsesordenen på de faktiske resultater af gangestykkerne.
Ad 4 – Gang andre 3-cifrede tal med 3-cifrede tal
Et andet gangestykke, hvor man ganger to 3-cifrede tal sammen er dette:
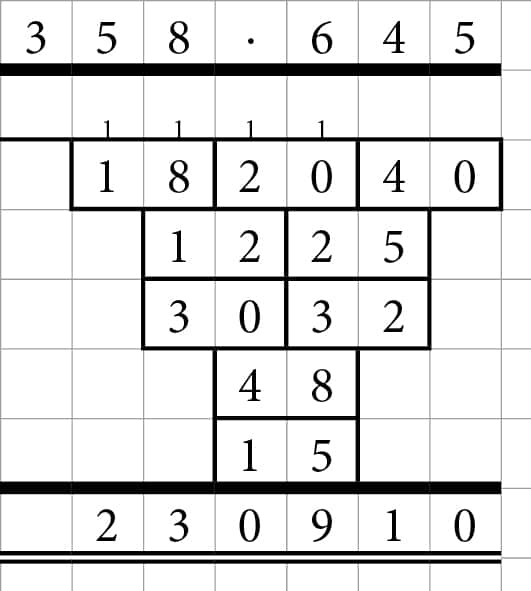
Ad 5 – Andre størrelser tal
Et eksempel på et gangestykke, hvor man ganger to 4-cifrede tal sammen:
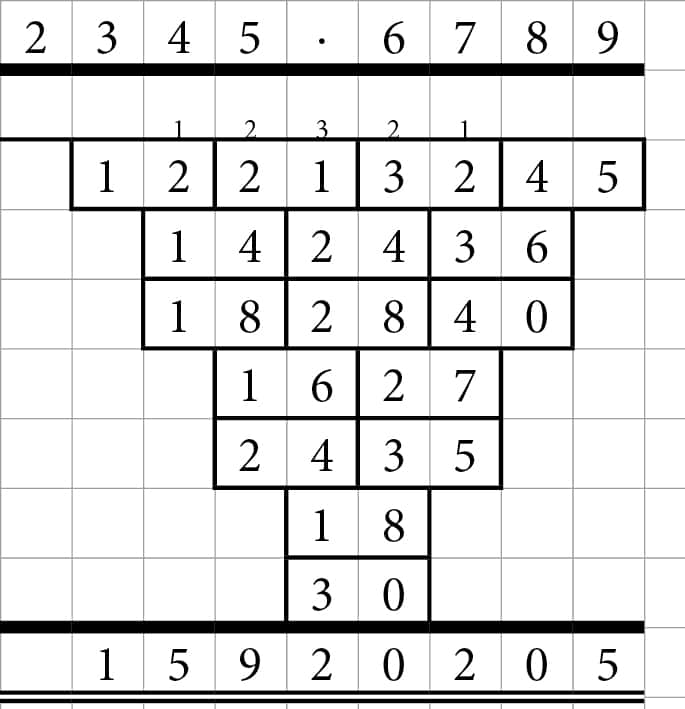
Et eksempel på et gangestykke, hvor man ganger to 5-cifrede tal sammen:
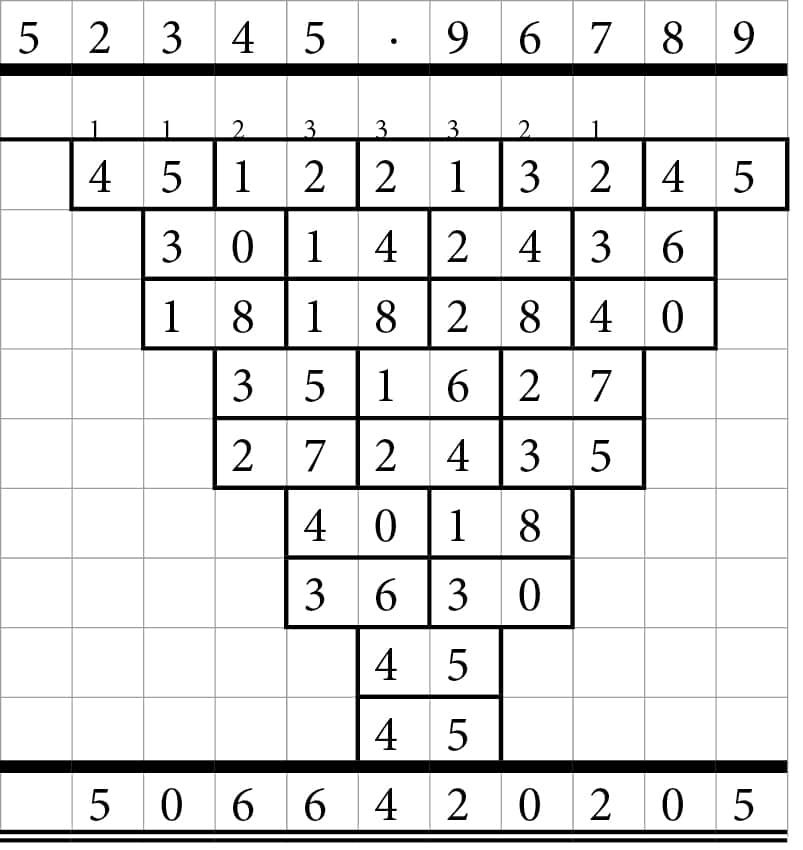
Et eksempel på et gangestykke, hvor man ganger to 2-cifrede tal sammen:
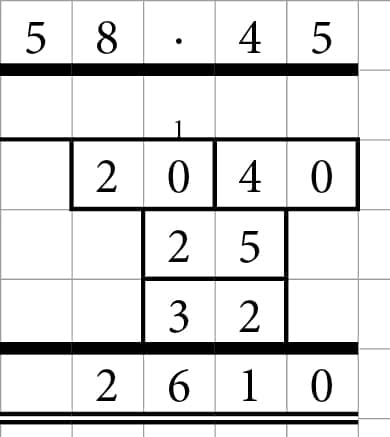
Ad 6 – Forskellige antal cifre
Når man ganger to tal, med forskellige antal cifre tager jeg udgangspunkt i et skema for det tal med flest cifre, og tilføjer et 0 på den manglende ciffers plads.
Et 4-cifret tal ganget med et 3-cifret tal ser for eksempel således ud:
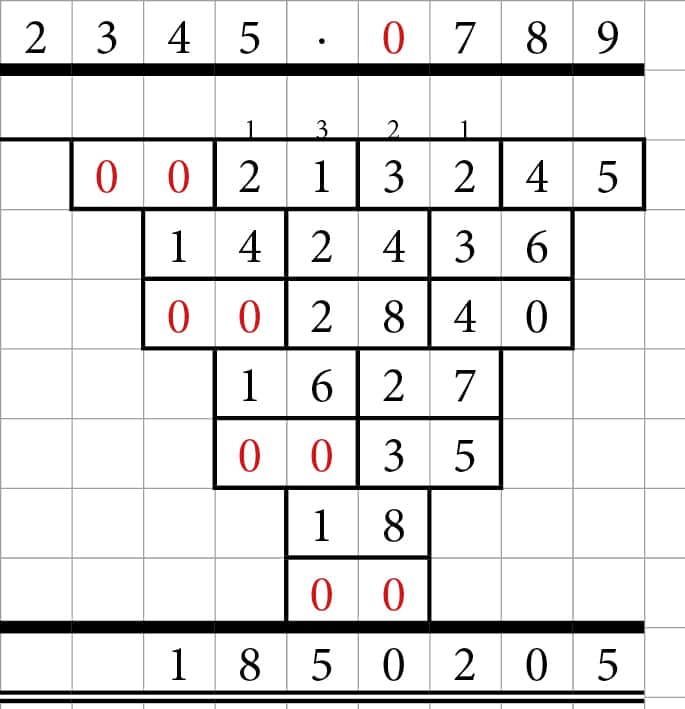
Ad 7 – 0 i tallene
0 volder som altid problemer, hvis man ikke tænker sig om, og husker hvor store tallene i virkeligheden er, men kun tænker i cifre.
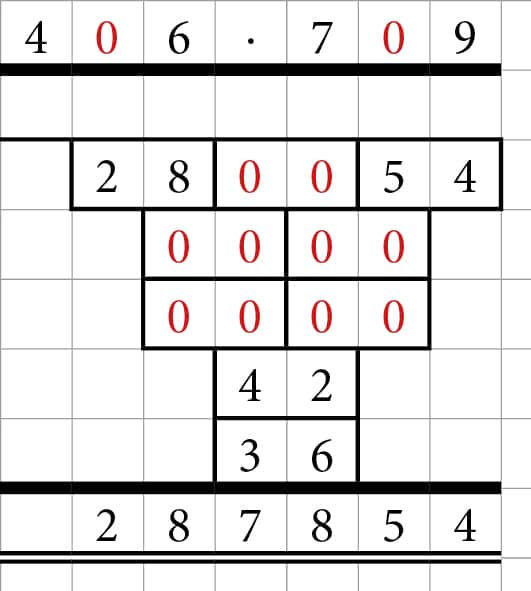
Ad 8 – Når produktet ikke er tocifret
Små cifre kan også give bøvl, når produktet ikke er 2-cifret. Igen skal man huske hvor store tallene i virkeligheden er.