Arbejde med et geometrisk bevis
Min gode ven og tidligere fagkonsulent, Klaus Fink, skrev følgende i et nummer af bladet Matematik:
”Vincenzo Vivianni (1622-1703) formulerede denne sætning: I en ligesidet trekant er summen af længderne på de tre vinkelrette linjestykker fra et vilkårligt punkt inde i trekanten lig med længden af højden i trekanten. Han beviste den selvfølgelig også. Kan du? Kan dine elever? Ja, selvfølgelig, og det er en god øvelse til udvikling af ræsonnementskompetencen.”
Jeg er nu ikke helt enig i ”Ja, selvfølgelig, og det er en god øvelse til udvikling af ræsonnementskompetencen.” Jeg synes ikke det er så selvfølgeligt at bevise og jeg er ikke så sikker på at det er en god øvelse i ræsonnementskompetencen for ret mange mennesker.
For det første bøvlede jeg selv noget med at lave et bevis. Jeg gjorde som Klaus senere i artiklen foreslår, og lavede konstruktionen i GeoGebra. Det kunne være gjort kønnere er jeg sikker på, med knap så mange gennemgående linjer, og måske færre linjer alt i alt, men jeg vidste jo ikke helt, hvad jeg ville. Jeg trak rundt med mine punkter, og det var fedt at summen af de nævnte tre linjestykker var lig med højden. Men som Klaus skriver, så er det jo ikke et bevis!
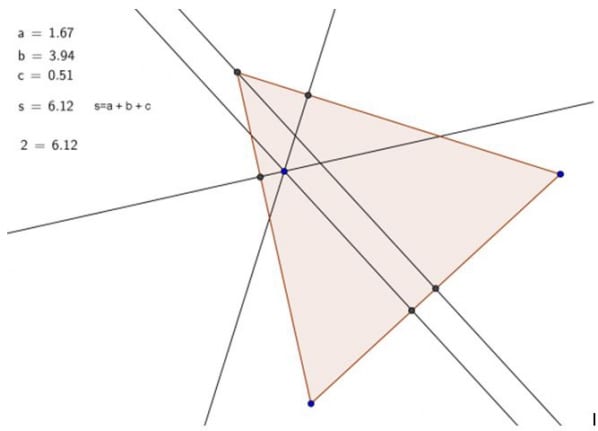
Så stirrede jeg på tegningerne for at se, om jeg kunne finde en smart måde at bevise det på. Det kunne jeg ikke! Så tegnede jeg lidt i hånd, for at se om det hjalp. Det gjorde det ikke. Så tænkte jeg skidt være med det, Pernille, nu regner du sku bare! Og et pænt stykke tid senere, med anvendelse af ligesidede trekanter, Pythagoras’ sætning og ligedannede figurer, så lykkedes det!
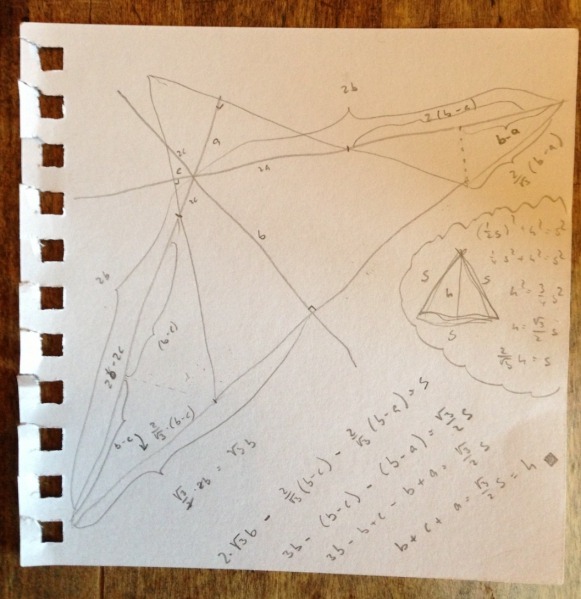
Først nu tillod jeg mig selv at google sætningen og to sekunder senere sad jeg med et smukt enkelt bevis fra Wikipedia:
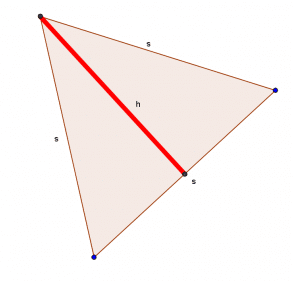
Man deler trekanten op i nedenstående tre trekanter:
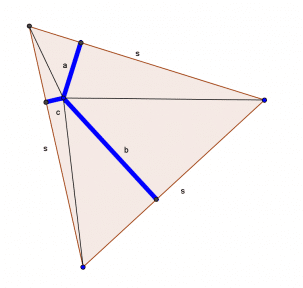
Og beregner summen af deres arealer:
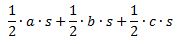
Sætter det lig med den oprindelige trekants areal:
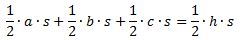
Ganger igennem med 2, dividerer med s og wupti, så er det der:
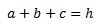
SMUKT! Men samtidig sad jeg med følelsen af ØV, det havde jeg ikke selv kunnet se! Og det er den reaktion, der er årsag til mit skriveri. Det er ødelæggende for læring af matematik når man dyrker “det geniale”. Alt for mange mennesker oplever følelsen “øv, det kunne jeg ikke” og det helt vandvittige er, at sådan en følelse får man også selv om man faktisk godt kunne finde ud af det! Man gjorde det måske bare på en lidt mere kringlet måde end den, man bliver præsenteret for af læreren og lærebøgerne. Og det med at kun at præsentere den geniale metode i lærebøgerne gælder ofte alt fra metoder til at trække to til fra hinanden til beviser for Vincenzo Viviannis sætning. Alt for sjældent præsenteres den bøvlede matematiske proces, der tager tid, kræver lidt gætteri, lidt prøven efter, lidt frem og noget tilbage, kræver at man kan holde styr på sin notation og sine udregninger. Men sådan er matematisk arbejde langt oftest. Gode matematikere har så viljen, stædigheden og fliden til at vende tilbage til samme problem, selvom de har løst det, fordi drømmen om den smukke løsning driver dem.
Jeg vil gerne være en god matematiker, så jeg vendte også tilbage og bøvlede med Vincenzo én gang til, og nu var min datter (som er PhD-studerende i matematik) kommet og kunne hjælpe med arbejdet. Jeg havde sat mig for at lave et geometrisk bevis. Når det smukke bevis baserede sig på arealer, var der noget der tydede på at et geometrisk bevis måtte være muligt. Sammen knoklede vi to timer, og kom tæt på, men ikke helt i land. Morgenen efter satte vi os igen og ret hurtigt fandt vi så endelig et smukt enkelt geometrisk bevis.
Vi printede de to udgaver af trekanten fra Wikipedia beviset på et hvidt stykke papir og et gult stykke papir, så vi i alt havde fire trekanter. Så klippede vi og samlede stumperne igen til to ens rektangler. Rektanglet med de blå linjer er samlet af tre rektangler med sidelængderne henholdsvis sidelængden på den ligesidede trekant og så de tre blå linjer. Med disse to rektangler bliver det tydeligt at de tre blå linjestykker tilsammen er lig med sidelængden af rektanglet, som også svarer til den røde højde i trekanten.
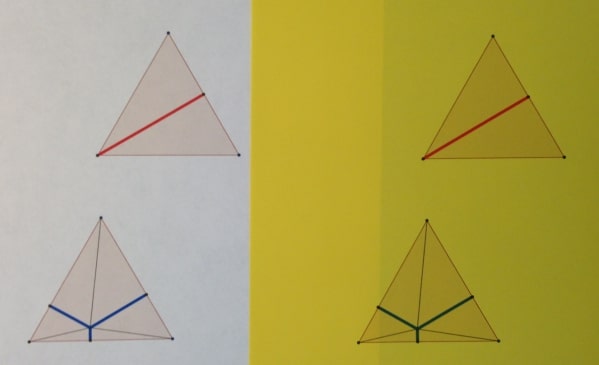
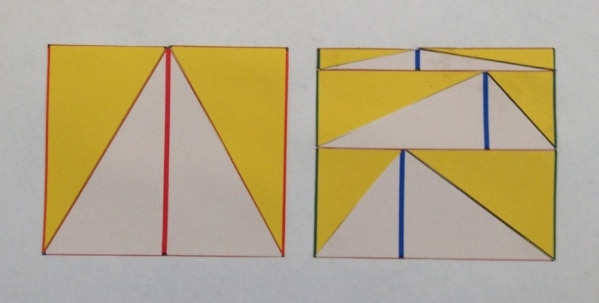
Jeg blev også nysgerrig efter udvidelser af sætningen:
Dur det i en vilkårlig trekant? Nej, det gør det ikke, for eksempel fordi der ikke er én højde i en vilkårlig trekant, men tre forskellige højder. Og prøver man den geometriske metode, kan man ikke samle stykkerne med de blå linjer til et kvadrat, det bliver til tre rektangler, der ikke har en fælles sidelængde.
Kan det udvides til andre regulære polygoner? Ja, på den måde at i en vilkårlig regulær n-kant er summen af afstanden fra et indre punkt til siderne lige med n gange radius af den indskrevne cirkel. Det kan man overbevise sig om geometrisk på lignende måde som ovenfor. Print nedenstående på to forskellige farvede papirer og klip og saml stykkerne til to rektangler med sidelængden som den ene sidelængde.
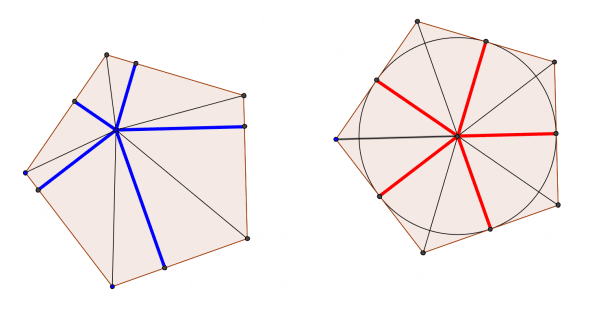
Tilbage til min oprindelige frustration over Klaus’ indledende bemærkning.
Jeg har to konkrete forslag for arbejdet med ræssonnementskompetencen for de nok ca. 95% af os, der ikke er geniale til matematik hele tiden:
- Lad os værdsætte bøvlet i langt højere grad end vi gør i dag. Lad os gøre det tydeligt i undervisningen at den matematiske proces er langsom og kringlet – og det er både smukt, rigtigt og værdifuldt. Gennem det bøvlede kommer ofte gode ræsonnementer og erfaringer, som kan bruges senere.
- Lad os præsentere de geniale beviser, som det de er: Noget enestående smukt, som er kommet frem efter meget bøvl, men som vi kan lære noget af, så vi næste gang har endnu flere redskaber at ræsonnere med. Og lad os snakke om hvad matematiske beviser egentlig er for noget. Hvorfor det for eksempel ikke er et matematisk bevis at prøve efter nogle gange og se at det passer. Ofte er det en bedre ide at vise det geniale bevis for eleverne, end at lade som om de selv kan komme frem til det – enten kan de ikke, eller så skal der så mange hints til at de egentlig ikke selv har været andet end penneførere.
Jeg må slutte med at takke Klaus for mange dejlige timer med Vincenzo Viviannis bevis. Som jeg håber at have gjort mere undervisningsparat med disse overvejelser.
Og endelig vil jeg også erklære mig enig med Klaus’ egentlige budskab i resten af indlægget: Tag nu og få etableret et godt fagligt team på skolen, fagligt samarbejde virker, skulle min datter og jeg hilse og sige.





