Voksende mønstre
Voksende mønstre er en herlig sammenblanding af geometri, tal og funktioner. Et voksende mønster er et geometrisk mønster, hvor man fokuserer på udvikling af mønsteret, og som en del af analysen af denne udvikling tilknytter man tal og forsøger at se et mønster i denne talfølge.
Man kan arbejde med voksende mønstre på alle klassetrin. I de yngste klassetrin er fokus mest på det geometriske, på mellemtrinnet kan tallene kobles på i højere grad, og på de ældste klassetrin kan man arbejde mere med talmønstrene og algebra.
Beskriv det geometriske mønster
Eleverne skal altid starte med at at sætte ord på det de ser. Hvordan ser mønsteret ud? Hvordan ser de første trin i udviklingen af mønsteret ud? Hvordan udvikler mønsteret sig derefter?
Et eksempel – vi kan kalde det firkantmønster:
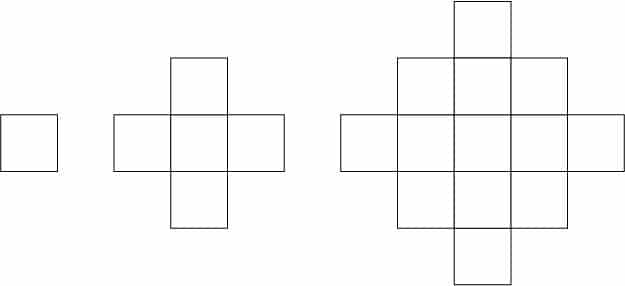
Indskoling – mellemtrin: “Det er firkanter, der er sat sammen. Man sætter hele tiden nogen udenom.”
Mellemtrin – udskoling: ”Det er et mønster af kvadrater. Det starter med et enkelt kvadrat. I hvert trin sættes der et kvadrat mere med samme sidelængde på alle de sider, hvor man kan.”
Tegn og fortsæt det geometriske mønster
At tegne mønsteret giver en anden forståelse end at sætte ord på. Måske opdager man nye facetter af mønsteret, som gør det tydeligere, hvordan mønsteret udvikler sig. Ved at tegne yderligere et par trin i det geometriske mønster kommer man endnu tættere på forståelsen af mønsteret. Det kan være en god ide at tage fotos af hvert trin i udviklingen af mønsteret, så man ikke behøver gentegne det hele ved hvert trin.
 |  |  |  |
| Trin 1 | Trin 2 | Trin 3 | Trin 4 |
Sæt tal på
Man kan undersøge et mønster ved at tælle et eller andet ved det og undersøge, hvordan dette antal vokser ved hvert trin. Man laver altså en talfølge, der beskriver mønstret. Man kan systematisere sine iagttagelser i en tabel. I firkantmønsteret kan man for eksempel se på antal tern:
| Trin nr | 1 | 2 | 3 | 4 |
| Antal tern | 1 | 5 | 13 | 25 |
Analyseredskaber til analyse af talfølger
Der er to redskaber, der altid er gode at bruge for at blive klogere på, hvilket mønster der er i en talfølge. Det ene er at se på forskelle mellem tallene og det andet er at se på forhold mellem tallene. Nogle gange kan det være en god ide at forsætte, og se på forskellenes forskel – eller forskellenes forhold. Man må prøve sig frem, indtil man ser et mønster.
Et eksempel med firkantmønsteret:
| Trin nr | 1 | 2 | 3 | 4 |
| Antal tern | 1 | 5 | 13 | 25 |
| Forskel | 4 | 8 | 12 | |
| Forskel | 4 | 4 |
Et eksempel med et andet mønster, vi kalder firkantfraktalmønster:
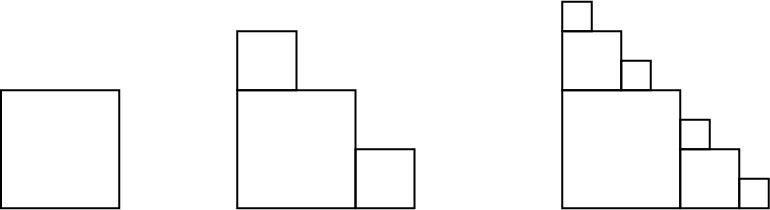
| Trin nr | 1 | 2 | 3 | 4 |
| Antal tern | 1 | 3 | 7 | 15 |
| Forskel | 2 | 4 | 8 | |
| Forhold | 2 | 2 |
Find det trinvise system i tallene
I undersøgelsen af, hvordan tallene vokser, prøver man at finde det trinvise mønster i tallene, altså en regel for hvordan man kommer fra tallet i et trin til tallet i det næste trin. Analyseredskaberne ovenfor kan være en hjælp. Man kan beskrive den trinvise regel rent sprogligt. Sådan starter alle elever typisk, og på mellemtrinnet er det også der, de elever fleste slutter. I udskolingen kan man gå videre og beskrive reglen i et mere abstrakt matematisk sprog, endelig kan nogle elever udfordres hen mod rent symbolsprog.
Eksempler med med firkantsmønsteret:
Rent sprogligt: Man skal hver gang bruge fire tern mere end man skulle sidste gang. Man skal altså lægge 4 mere til hver gang. Først plus 4, så plus 8, så plus 12 og så videre.”
Mere abstrakt matematisk, for eksempel:
Næste tal = gammelt tal + 4-tabel eller
Næste tal = gammelt tal + 4 · (trinnummeret før) eller
Næste tal = gammelt tal + 4 · (trinnummeret – 1) eller
Næste tal = gammelt tal + yderste ring i gammel figur + 4 eller
A(n) = A(n – 1) + (A(n – 1) – A(n – 2)) + 4, hvor A(n) betyder antal tern i trin nummer n.
Disse trinvise regler er gode at udnytte i regneark, til at få regnet lige så langt frem man ønsker.
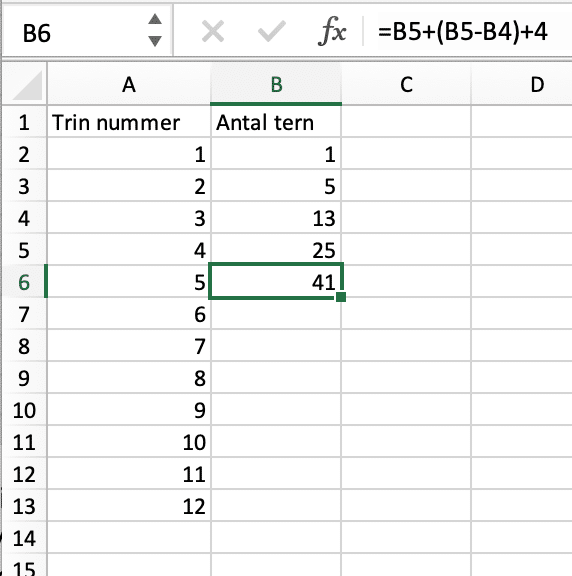
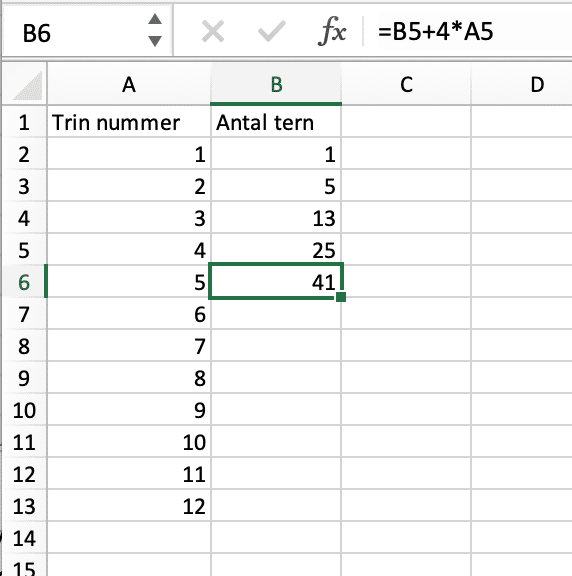
Find en generel formel
Med en trinvis regel kan man regne sig lige så langt frem som man ønsker ved at tage ét trin ad gangen. Med et regneark til hjælp, kan det oven i købet gå rimelig hurtig. Men det er en god øvelse i algebra at prøve at finde en generel formel, altså en formel der giver tallet for trin nummer n, uden at skulle regne alle de forudgående trin ud først. Der er flere veje at gå for at finde en generel formel.
Se på forskelle og forhold
Lineær funktion
Når forskellen mellem to trin er det samme hele tiden, altså konstant, er den generelle formel en lineær funktion. Den konstante forskel er a-værdien i et lineært udtryk a · n + b. b-værdien kan man finde ved at bruge den fundne a-værdi og en kendt sammenhæng mellem trinnummer og funktionsværdi. At den konstante forskel er a kan man regne sig frem til på denne måde:
| Trin nr | n | n+ 1 |
| Antal | a · n + b | a · (n + 1) + b |
| Forskel | a · (n + 1) + b – (a · n + b) = a · n + a + b – a · n- b = a |
Et eksempel med dette mønster:

| Trin nr | 1 | 2 | 3 |
| Antal kanter | 4 | 7 | 10 |
| Forskel | 3 | 3 |
Heraf ses, at a = 3. Ved at sætte n = 1 ind i 3 · n + b og bruge, at antal kanter i trin nummer 1 er 4, får man at b = 1 da 3 · 1 + 1 = 4. Den generelle formel er da 3 · n + 1.
Andengradsfunktion
Når forskellenes forskel er konstant, er der en sammenhæng af anden grad, altså noget med n2. Koefficienten til n2 (altså a-værdien i a · n2+ b · n + c ) er halvdelen af den ovenfor nævnte konstant. De to andre konstanter b og c kan man finde ved at bruge den fundne a-værdi og to kendte sammenhænge mellem trinnummer og funktionsværdier, og løse dette ligningssystem. Når man ved der er en andengradssammenhæng kan man også finde den generelle formel ved at bruge regression i regneark. At a-værdien er halvdelen af forskellenes forskel, kan man regne sig frem til på denne måde:
| Trin nr | n | n + 1 | n + 2 |
| Antal | a · n2+ b · n + c | a · (n + 1)2+ b · (n + 1) + c | a · (n + 2)2+ b · (n + 2) + c |
| Forskel | a · (n + 1)2+ b · (n + 1) + c – (a · n2+ b · n + c) = a · 2n + a + b | a · (n + 2)2 + b · (n + 2) + c – (a · (n + 1)2 + b · (n + 1) + c) = a · 2n+ 3a + b | |
| Forskel | a · 2n + 3a + b – (a · 2n + a + b) = 2a |
Eksempel med firkantmønsteret:
| Trin nr | 1 | 2 | 3 | 4 |
| Antal tern | 1 | 5 | 13 | 25 |
| Forskel | 4 | 8 | 12 | |
| Forskel | 4 | 4 |
a er halvdelen af 4, altså 2. Ved at bruge, at antal tern ved trinnummer 1 er 1 og antal tern ved trinnummer 2 er 5 får man disse to ligninger for b og c: 2 · 12 + b · 1 + c = 1 og 2 · 22 + b · 2 + c = 5 som kan reduceres til b + c = -1 og 2b + c = -3. Det giver b = -2 og c = 1. Den generelle formel er da 2 · n2 – 2n + 1.
Tredjegradsfunktion
Når forskellen på forskellenes forskel er konstant, er der en tredjegradssammenhæng dvs. noget med n3. Koefficienten til n3 er den ovenfor nævnte konstant divideret med 6. Beviset for det får man ved at regne ligesom ovenfor, bare lidt mere…
Et eksempel med dette firkantpyramidemønster:
 |  |  |
| Trin 1 | Trin 2 | Trin 3 |
| Trin nr | 1 | 2 | 3 | 4 | 5 |
| Antal kuber | 1 | 5 | 14 | 30 | 55 |
| Forskel | 4 | 9 | 16 | 25 | |
| Forskel | 5 | 7 | 9 | ||
| Forskel | 2 | 2 |
Her bliver koefficienten til n3 altså 2/6 = 1/3.
Ved brug af regression i forhold til et tredjegradspolynomium i regneark kan man se, at den generelle formel er 1/3n3 + 1/2n2 + 1/6n.
Eksponentiel udvikling
Når forholdet mellem to trin er konstant, er der tale om en eksponentiel udvikling altså noget med an. At a-værdien er det konstante forhold kan man regne sig frem til på denne måde:
| Trin nr | n | n + 1 |
| Antal | an | a(n + 1) |
| Forhold | a(n + 1) / an= a |
Et eksempel med dette mønster:

| Trin nr | 1 | 2 | 3 | 4 |
| Antal tern | 1 | 3 | 7 | 15 |
| Forskel | 2 | 4 | 8 | |
| Forhold | 2 | 2 |
Forskellen kan beskrives ved an med a = 2 altså 2n. Den generelle formel for antal tern er ikke præcis 2n, da vi først havde fundet forskellen, men ved at se lidt nærmere på tallene kan man se, at de generelle tal er én mindre end forskellene, så den generelle formel er 2n– 1.
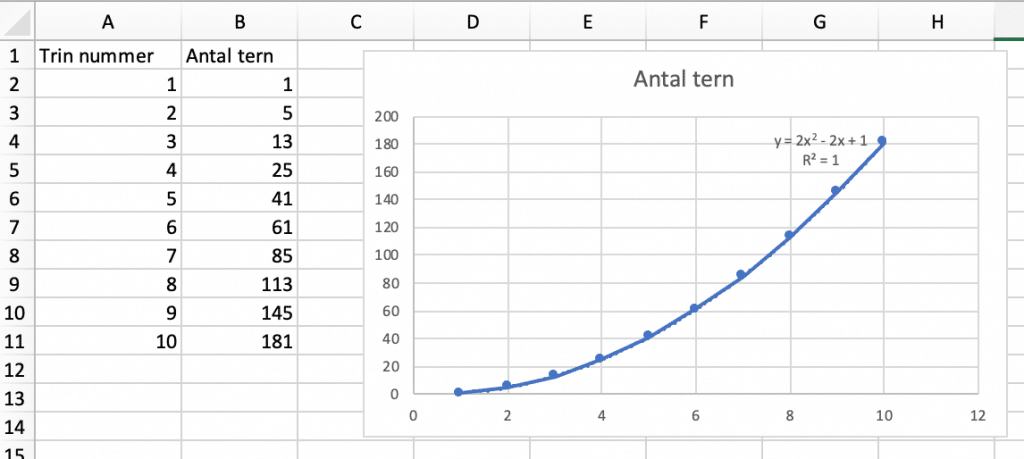
Se på grafen
Man kan vælge at få et nyt blik på sine tal ved at lave et grafisk billede af dem ved at indsætte tabelværdierne i et koordinatsystem.
Er man vant til at se på det grafiske billede af forskellige funktioner, vil man ofte kunne genkende, om det grafiske billede repræsenterer en lineær funktion, en andengradsfunktion, en tredjegradsfunktion eller en eksponentiel vækst. For at finde den generelle formel kan man anvende regression i et regneark. Og er man i tvivl om hvilken type funktion, man skal bruge, kan man jo eksperimentere sig frem og se hvilken type der passer bedst med tallene.
Se på mønsteret rent geometrisk
Det er også en dejlig udfordring at prøve at se om man kan se den generelle formel rent geometrisk. Man skal i mønsteret lede efter firkanter eller trekanter, der kan sættes sammen til firkanter, da det er let at tælle brikker i noget firkantet ved at sige det ene led ganget det andet led.
Vi bruger firkantmønsteret som eksempel igen. Man kan farve mønsteret sort og hvidt som et skakternet flisegulv, og derefter vende mønsteret på skrå og se på de sorte og hvide brikker hver for sig.
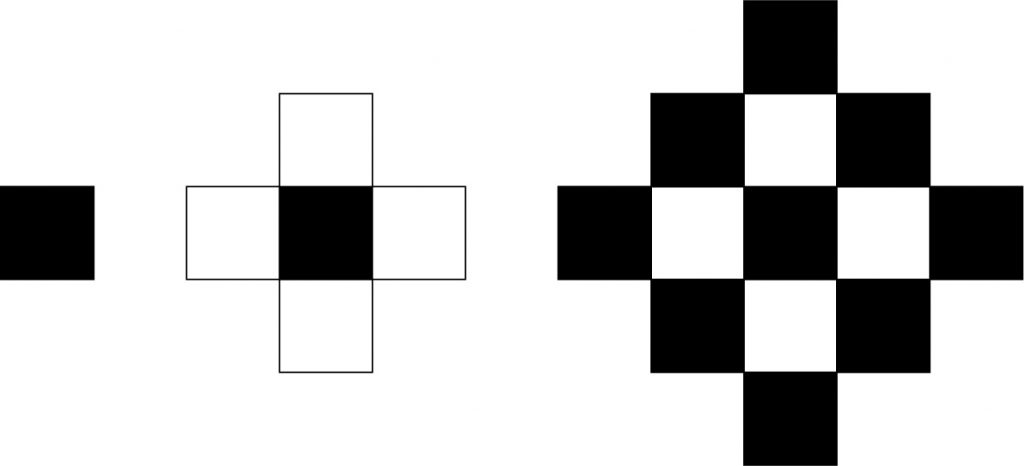
Med lidt god vilje kan man da se, at der er et sort kvadrat og et hvidt kvadrat. Det giver for trin nummer n: n2+ (n – 1)2. Hvilket er det samme som formlen 2n2 – 2n + 1, som vi har fundet før.
Man kan også bruge geometrien til at få en ide om den generelle formel er noget lineært med n, noget andengrads med n2 eller noget tredjegrads med n3. Hvis mønsteret kun vokser i længden, som for eksempel trekanter på linje, kan den generelle formel være lineær, altså noget a · n + b. Vokser mønsteret i to dimensioner, så det dækker et areal, som for eksempel firkantmønsteret, så kan den generelle formel være en andengradsfunktion, altså noget med n2 (ligesom i kvadratmeter m2). Og endelig, hvis mønsteret vokser i tre dimensioner, som for eksempel firkantpyramidemønsteret, så det fylder et rum, så kan den generelle formel være en tredjegradsfunktion, altså noget med n3 (ligesom i kubikmeter m3).
Afsluttende bemærkninger
Før du arbejder med voksende mønstre med dine elever skal du overveje, hvilke mønstre, der er passende udfordringer for dine elever. På de yngste klassetrin er det nok en god ide at nøjes med mønstre, der kun vokser i én dimension. På mellemtrinnet kan man tage de mønstre med, der vokser som en andengradsfunktion, men undlade fraktalmønstrene og de tredimensionelle mønstre. I udskolingen kan alle mønstrene medtages.
Hvilke værktøjer er den bedste hjælp i analysen for dine elever? Er det mønsterpapir, tændstikker eller andre konkreter, kamera til at fotografere trin, tabelskabeloner med forskel, forskellenes forskel mm. og/eller regneark? Det er nok en god ide at lære dine elever om analyseredskaberne forskel, forskellenes forskel og eventuelt forhold inden de går i gang med et eksempel.
Og lad så eleverne komme i gang!
Elevmateriale kan downloades her.
Analyseskabelon kan downloades her.
Mønsterpapir (trekanter) kan downloades her.
Mønsterpapir (firkanter) kan downloades her.
Mønsterpapir (sekskanter) kan downloades her.





